Kurz- und langfristige Effekte einer entwicklungsorientierten Mathematikförderung bei Erstklässlern mit drohender Rechenschwäche
Abstract
Kinder mit schwach entwickelten mathematischen Basiskompetenzen haben ein deutlich erhöhtes Risiko für die Entwicklung einer Rechenschwäche. Mathematische Basiskompetenzen werden daher nicht nur als wichtiges Kriterium für die Früherkennung entsprechender Fehlentwicklungen gesehen, sondern sie gelten als besonders vielversprechender Ansatzpunkt für präventive Maßnahmen. Allerdings existieren bislang kaum Programme, deren langfristige Wirksamkeit als empirisch gesichert gelten kann. In der vorliegenden Studie sollte daher die Effektivität eines Förderprogramms bei Risikokindern in der ersten Klasse überprüft werden. Aus einer Gesamtstichprobe von 238 Erstklässlern wurden mit Hilfe eines Tests zur Erfassung mathematischer Basiskompetenzen 64 Kinder ausgewählt, die ein erhöhtes Risiko zur Entwicklung einer Rechenschwäche aufwiesen. Die Hälfte der Risikokinder wurde der Trainingsgruppe zugeteilt, die über fünf Wochen hinweg mit zehn ausgewählten Sitzungen des Programms „Mengen, zählen, Zahlen“ (Krajewski et al., 2007) gefördert wurde. Die andere Hälfte bildete die Kontrollgruppe und absolvierte im selben Zeitraum das konventionelle Förderangebot der Schule. Wie die Ergebnisse zeigen, erzielte die Trainingsgruppe im Verlauf der Förderung substanziell größere Zugewinne in ihren mathematischen Basiskompetenzen als die Kontrollgruppe. Die Vorteile der Trainingsgruppe erwiesen sich als zeitlich stabil und hatten auch drei Monate nach Abschluss der Förderung noch Bestand. Darüber hinaus schlug sich die Förderung langfristig auch in einer verbesserten Rechenleistung der Kinder nieder. Dieser Transfereffekt war allerdings noch nicht unmittelbar nach Abschluss der Förderphase sichtbar, sondern trat erst nach einer zeitlichen Verzögerung zutage. Es handelt sich somit um einen „Sleeper-Effekt“, der darauf hindeutet, dass die MZZ-geförderten Risikokinder aufgrund ihrer trainingsbedingt verbesserten Basiskompetenzen nachfolgend auch vom regulären Mathematikunterricht besser profitieren konnten.
Background: Early deficits in quantity-number competencies (QNC) are closely related to subsequent problems in mathematical school achievement. As demonstrated by recent longitudinal studies, quantity-number competencies assessed in kindergarten or immediately after school entry are the strongest predictors of mathematical achievements at the end of grade 4, even if relevant third variables like intellectual ability or calculation skills are controlled (e. g. Ennemoser et al., in press). Thus, fostering quantity-number competencies seems a promising approach for the prevention of mathematical difficulties. However, as there is a lack of evaluation studies, little is known about the effectiveness of available QNC-trainings. Moreover, although most prevention programs in mathematics education claim to stimulate the fundamentals of subsequent mathematical achievement (often referred to as “number sense” or mathematical “precursors”), they often lack a sound theoretical basis on the development of early mathematical competencies. One prevention approach that is strictly based on a well-established theory of mathematical development, and therefore seems particularly suitable to foster quantity-number competencies, is the program Mengen, zählen, Zahlen (Quantities, counting, numbers; MZZ; Krajewski et al., 2007). Although the MZZ training was originally designed for kindergarten classes (i. e. as a means of primary prevention), it is increasingly used as a small-group training for school children at risk (i. e. as a means of secondary prevention). While there is rapidly growing evidence that suggests the efficacy of this program both in kindergarten and post-school entry, only a few studies investigated the durability of training gains or transfer effects to subsequent mathematical achievement, respectively.
Aims: The aim of the current study was to investigate the effectiveness of the QNC-training Mengen, zählen, Zahlen (Krajewski et al., 2007) in first-grade children who are at-risk of developing mathematical difficulties. Both short-term and long-term effects were examined. Furthermore, it was examined whether training-induced gains in quantity-number competencies actually transfer to subsequent development of calculation skills which were explicitly not taught during the QNC-training.
Method: Based on their low performance in a standardized QNC test, 62 out of 238 first-graders were identified as being at risk of developing mathematical difficulties, and assigned to either the training group (n = 32), or the control group (n = 32). The training group participated in the MZZ program comprising 10 training sessions over the course of five weeks. During the same time the control group received remedial mathematical instruction provided by the school. Quantity-number competencies as well as calculation skills were assessed by standardized achievement tests at three measurement points (pretest, posttest, follow-up test three months after training). In addition, nonverbal IQ was assessed in order to control for effects of intellectual ability.
Results: At posttest the training group significantly outperformed the control group in a standardized test of quantity-number competencies with a medium effect size of d = 0.64. According to our expectations, this effect remained stable over time, i. e. the training group still displayed superior quantity-number competencies three months after intervention (d = 0.69). While there was no transfer effect on calculation skills immediately after intervention, the training group subsequently showed larger improvements in their calculation skills than the control group. Until follow-up assessment three months after intervention, the advantage of the training group was statistically significant with a medium effect size of d = 0.52. The time-lagged transfer effect of MZZ training on the development of calculation skills was partially mediated by training-induced profits in quantity-number competencies. This “sleeper effect” is theoretically plausible and indicates that precedent progress in basic quantity-number competencies subsequently leads to more efficient learning during regular mathematics instruction.
Discussion: The results of our study add to the growing body of research suggesting that intervention programs to foster quantity-number competencies are a promising means of effective prevention. They particularly demonstrate the effectiveness of the strictly theory-based QNC-training MZZ used in this study. Both short-term and long-term effects were found as well as transfer effects on subsequent development of mathematical skills. It seems important to note that these effects were found for a training that was originally designed as a pre-school prevention program. The training does not contain any symbolic calculation tasks and mainly focuses on the comprehension of the linkage between quantities and numbers. Thus, our findings also impressively underscore the fundamental relevance of quantity-number competencies usually acquired before school entry. Children who were not able – or did not have the opportunity – to attain these competencies can be effectively supported by QNC-training not only during kindergarten but also after entry into formal mathematics instruction.
Einleitung
Während die Lese-Rechtschreibforschung in den letzten Jahrzehnten ein immenses Forschungsvolumen auf sich vereinen konnte, blieb die Erforschung der mathematischen Kompetenzentwicklung dem gegenüber für lange Zeit weit zurück. Erst in den letzten Jahren ist eine deutliche Zunahme des Publikationsumfangs in diesem Bereich zu beobachten. Dabei liegt ein besonderer Fokus auf den frühen Phasen der mathematischen Kompetenzentwicklung (vgl. Krajewski & Ennemoser, 2013). Hinter der Konzentration auf frühe Erwerbsphasen verbirgt sich die Hoffnung, dass es – ähnlich wie im Bereich der Lese-Rechtschreibforschung – gelingt, so genannte Vorläuferfertigkeiten im Sinne mathematischer Basiskompetenzen zu identifizieren. Denn zum einen eröffnet die Kenntnis solcher Vorläuferfertigkeiten die Möglichkeit mathematikspezifische Entwicklungsrisiken bereits früh zu erkennen. Und zum anderen stellen Vorläuferfertigkeiten naturgemäß einen vielversprechenden Ansatzpunkt für Präventionsmaßnahmen dar, die es im Idealfall ermöglichen, einer drohenden Rechenstörung bereits wirksam entgegenzutreten, noch bevor sie sich überhaupt manifestieren kann. Tatsächlich ist es in den letzten Jahren gelungen diesbezüglich einige Fortschritte zu erzielen. Eine wesentliche Grundlage hierfür stellen theoretische Modellierungen der mathematischen Kompetenzentwicklung dar, aus denen sich ableiten lässt, welche Meilensteine auf dem Weg zum kompetenten Rechner bewältigt werden müssen.
Bevor wir im Folgenden näher auf ein entsprechendes Entwicklungsmodell eingehen, soll noch kurz die Verwendung einiger Begrifflichkeiten erläutert werden, um etwaigen Verwirrungen vorzubeugen. Als Sammelbegriff für sehr grundlegende mathematische Fähigkeiten und Fertigkeiten hat sich in der Literatur der Begriff „mathematische Basiskompetenzen“ etabliert. Leider ist der Begriff – sowohl in der deutschsprachigen Version als auch in der internationalen Entsprechung („number sense“; z. B. Gersten, Jordan & Flojo, 2005) sehr unscharf definiert. Die hierunter subsummierten Kompetenzen reichen von pränumerischen Einsichten über die Beherrschung halbschriftlicher Rechenverfahren bis hin zu einem grundlegenden Verständnis der mathematischen Notation in der Sekundarstufe (vgl. Ennemoser, Krajewski & Schmidt, 2011). Da es in der vorliegenden Studie explizit um frühe Vorläuferfertigkeiten geht, die von einem Großteil der Kinder bereits vor dem Schuleintritt erworben werden, verwenden wir an dieser Stelle – in Anlehnung an das nachfolgend erläuterte Entwicklungsmodell – bevorzugt den etwas präziseren Begriff der „Zahl-Größen-Kompetenzen“.
Entwicklungsmodell der Zahl-Größen-Verknüpfung (ZGV-Entwicklungsmodell)
Ein aktuelles Entwicklungsmodell, das auf einer breiten Analyse des internationalen Forschungsstandes basiert, ist das Modell der Zahl-Größen-Verknüpfung (Krajewski, 2005, 2007, 2013). Als besonders relevanter Meilenstein – und damit auch als potenzielle Entwicklungshürde – wird hier der schrittweise Aufbau des Verständnisses für die Verknüpfung zwischen Zahlen und Größen bzw. Mengen verstanden. Den Modellvorstellungen folgend lässt sich der Erwerb dieses Verständnisses auf drei Ebenen verorten.
Zahlwörter und Ziffern ohne Größenbezug (Ebene 1)
Bereits Säuglinge sind dazu in der Lage zu beurteilen, ob sich Objekte beziehungsweise (numerisch unbestimmte) Mengen in ihrer räumlichen Ausdehnung unterscheiden. Unabhängig von diesem intuitiven, zahlunabhängigen Größenverständnis erlernen Kinder ab dem Kleinkindalter das Zählen. Die Kenntnis von ersten Zahlwörtern sowie das Aufsagen einer kurzen Zahlwortfolge einerseits und die Fähigkeit zur Beurteilung von Mengen und Größenausdehnungen andererseits werden aber noch nicht zwingend miteinander in Verbindung gebracht. Wenn Kinder in dieser Phase der Entwicklung beispielsweise vier Finger ihrer Hand abzählen, können sie möglicherweise auf den betreffenden Finger zeigen und feststellen, dass dieser Finger „die Vier“ ist. „Die Vier“ wird hierbei jedoch noch nicht zwingend als das Gesamt aller bis hierhin gezählten Finger, also als deren Anzahl, verstanden. Vielmehr wird das Zahlwort lediglich als eine Art Label verwendet, mit dem immer der Gegenstand (in diesem Falle der betreffende Finger) bezeichnet wird, bei dem das Kind während des Zählens bis zu diesem Zeitpunkt angelangt ist.
Zahl-Größen-Verknüpfung (Ebene 2)
Erst allmählich, im Verlauf des Kindergartenalters, beginnen Kinder die Verknüpfung zwischen Zahlen und Mengen bzw. Größen zu verstehen. Dabei handelt es sich anfangs noch um ein sehr vages, unpräzises Verständnis (unpräzises Anzahlkonzept; Ebene 2a). Die Kinder lernen nach und nach, dass manche Zahlen mit verbalen Begriffen wie „wenig“ korrespondieren und damit nur kleine Mengen repräsentieren, während andere Zahlen mit Begriffen wie „viel“ oder „sehr viel“ assoziiert sind, also mit großen oder gar sehr großen Mengen oder Größen in Verbindung gebracht werden. So mag beispielsweise die Zahl zwei in die verbale Kategorie „wenig“ fallen, wohingegen die Zahl „tausend“ als „sehr viel“ aufgefasst wird. Die verbalen Größenbezeichnungen (wenig – viel – sehr viel) sind natürlich nur sehr grobe Kategorien, die keine klar definierten Zahlenbereiche umfassen. Zudem können Kinder zwischen Zahlen, die innerhalb derselben Größenkategorie liegen, nicht zuverlässig differenzieren. Wenn ein Kind beispielsweise die Zahlwörter sechzehn und neunzehn in dieselbe Kategorie „viel“ einordnet, so kann es keine kompetente Größenunterscheidung zwischen diesen beiden Zahlwörtern treffen (z. B. auf die Frage, ob sechzehn größer oder kleiner ist als neunzehn). Dies gelingt ihm erst in der Phase des präzisen Anzahlkonzepts. Hier können Kinder nun abzählbare Mengen auch exakt in die Zahlenfolge einordnen (achtzehn sind mehr als siebzehn und beide sind weniger als neunzehn).
Zahlrelationen (Ebene 3)
Erst auf der Ebene der Zahlrelationen werden die bereits früh vorhandenen Kompetenzen zur Beurteilung von Relationen zwischen numerisch unbestimmten Mengen und Größen mit den Zahlwörtern verknüpft. Die Kinder verstehen nun, dass – wenn man eine größere Menge in zwei Teilmengen zerlegt – sowohl die Teilmengen als auch, darüber hinausgehend, die Relation zwischen diesen Teilmengen mithilfe von Zahlen darstellbar sind, also exakt quantifiziert werden können. Konkret fällt hierunter die Fähigkeit zu erkennen, dass die Anzahl „acht“ in die Anzahlen „fünf“ und „drei“ zerlegbar ist und dass die Teilmenge „fünf“ genau „zwei mehr“ umfasst als die Teilmenge „drei“. Zentral ist, dass diese Sachverhalte auf Zahl(wort)ebene grundsätzlich verstanden sind. Die Durchführung entsprechender Operationen auf Symbolebene (etwa in der Form 5 = 8 − 3) muss noch nicht beherrscht werden.
Das ZGV-Modell ist kompatibel mit den Grundannahmen des sehr populären neuropsychologischen Modells von Dehaene (1992), das allerdings keine Entwicklungsperspektive verfolgt. Im Rahmen dieses Modells werden drei Arten der Zahlenrepräsentation unterschieden, die flexibel ineinander überführt werden können beziehungsweise müssen (analoge Größenvorstellung, sprachliche und visuell-arabische Zahlvorstellung). Analogien zum ZGV-Modell betreffen insbesondere das Transkodieren von Zahlwörtern bzw. Ziffern in die entsprechenden analogen Größenrepräsentationen und umgekehrt. Dabei liefert das ZGV-Modell eine Beschreibung dafür, wie sich die Zuordnung von Zahlwörtern (bzw. Ziffern) zu Größenrepräsentationen im Entwicklungsverlauf überhaupt erst herausbildet.
Neben dem dargestellten Entwicklungsmodell der Zahl-Größen-Verknüpfung existieren noch weitere entwicklungspsychologische Theorien und Modellvorstellungen, die – an einigen Stellen nur im Detail, an anderen durchaus fundamental – andere theoretische Grundpositionen vertreten als das ZGV-Modell (z. B. Fuson, 1988; von Aster & Shalev, 2007). Der wichtigste Unterschied zum ZGV-Modell besteht in dem hier vorliegenden Grundprinzip minimalistischer Kompetenzzuschreibungen (Krajewski & Ennemoser, 2013). Dieses Prinzip beinhaltet, dass Leistungen, die bei einem Kind beobachtet werden können, im ZGV-Modell stets konservativ interpretiert werden um zu vermeiden, dass die mathematischen Kompetenzen eines Kindes systematisch überschätzt werden (Krajewski & Ennemoser, 2013). Beispielhaft kann hier das Aufsagen von separaten Zahlwörtern genannt werden. Während andere Forscher (z. B. Fuson, 1988; von Aster & Shalev, 2007) allein aus dem Aufsagen von Zahlwörtern schließen, dass die betreffenden Kinder diese Zahlwörter üblicherweise bereits mit Mengen und Größen verknüpfen und damit ein erstes konzeptuelles Zahlverständnis demonstrieren (vgl. oben: Ebene 2), gilt dieser Schluss im ZGV-Modell als unzulässig. Stattdessen wird argumentiert, dass Zahlwörter – wie im Übrigen jedes andere Wort auch – durchaus von Kindern „nachgeplappert“ und wiederholt werden können, ohne dass der Sinn dieses Wortes exakt verstanden sein muss. Deshalb erfolgt die Verortung dieser Kompetenz (des Aufsagens von Zahlwörtern) hier auf einer lediglich sehr basalen Ebene (Ebene 1). Mit dieser Sichtweise einer minimalistischen Kompetenzzuschreibung eröffnet das ZGV-Modell Ansatzpunkte für die Förderung, die bei einer unzulässig optimistischen Interpretation kindlicher Leistungen leicht übersehen werden und dementsprechend keine hinreichende Berücksichtigung in der Konzeption von Fördermaßnahmen finden. Aus obigem Beispiel lässt sich ableiten, dass das Verständnis für die Verknüpfung von Zahlen mit Mengen, Stückzahlen und Größen nicht als „gegeben“ vorausgesetzt werden sollte, sondern dass Kinder dieses im Laufe ihrer Entwicklung erst erwerben müssen, selbst wenn es manchen – aber eben längst nicht allen – Kindern intuitiv und scheinbar ohne Mühe gelingt sich dieses Verständnis anzueignen. Aus diesem Grunde setzt eine Förderung, die sich an den Prinzipien des ZGV-Modells orientiert (siehe unten: „Mengen, zählen, Zahlen“, Krajewski, Nieding & Schneider, 2007), konsequenter Weise auf einer viel basaleren Verständnisebene an als dies alternative Ansätze tun.
Prognostische Relevanz spezifischer Vorläuferfertigkeiten
Der praktische Nutzen eines Entwicklungsmodells bemisst sich unter anderem daran, wie gut die theoretisch als relevant erachteten Basiskompetenzen tatsächlich dazu geeignet sind, den späteren Lernerfolg im Fach Mathematik vorherzusagen. Bezogen auf die im Sinne des oben dargestellten ZGV-Entwicklungsmodells definierten Zahl-Größen-Kompetenzen liefert die internationale Forschung vergleichsweise konsistente Belege dafür, dass diese bereits vor beziehungsweise kurz nach Schuleintritt eine recht zuverlässige Vorhersage der späteren Mathematikleistungen in der Grundschulzeit erlauben (Aunola, Leskinen, Lerkkanen & Nurmi, 2004; Jordan, Glutting & Ramineni, 2010; Krajewski, 2003; Krajewski & Schneider, 2009a, Krajewski & Schneider, 2009b; Locuniak & Jordan, 2008; Moeller, Pixner, Zuber, Kaufmann & Nuerk, 2011; Stern, 1997; Passolunghi, Vercelloni, & Schadee, 2007; von Aster, Schweiter & Weinhold-Zulauf, 2007). Zudem liegen Befunde vor, wonach auch Defizite rechenschwacher Grundschüler noch auf Problemen im Bereich dieser grundlegenden Zahl-Größen-Kompetenzen beruhen (Gaupp, Zoelch & Schumann-Hengsteler, 2004; Geary, Hamson & Hoard, 2000; Landerl, Bevan & Butterworth, 2004). Moser-Opitz (2007) konnte selbst bei rechenschwachen Fünft- und Achtklässlern Schwierigkeiten mit arithmetischen Operationen (Ergänzen sowie Verdoppeln und Halbieren) feststellen, die auf in der Regel früh verfügbaren Zahl-Größen-Kompetenzen wie dem Verständnis für Anzahldifferenzen und dem Teil-Ganzes-Verständnis beruhten (vgl. ZGV-Modell, Kompetenzebene 3). Insbesondere geht aus aktuellen Längsschnittstudien zur Validierung von diagnostischen Verfahren zur Erfassung mathematischer Basiskompetenzen hervor, dass die mathematische Leistungsentwicklung über die gesamte Grundschulzeit hinweg mithilfe der entsprechenden Testinstrumente zuverlässig vorhergesagt werden kann (MBK 1+; Ennemoser, Krajewski & Sinner, in Druck; MBK 0; Krajewski, in Druck). Die hierbei vorgelegten Befunde zeigen eindrucksvoll, dass die Mathematikleistung im Allgemeinen und Rechenschwierigkeiten im Besonderen selbst über einen Zeitraum von vier bis fünf Jahren hinweg substanziell durch die vor und unmittelbar nach dem Schuleintritt erfassten Zahl-Größen-Kompetenzen prognostizierbar sind. Deren herausragender prognostischer Stellenwert bleibt auch bei Kontrolle relevanter Drittvariablen, wie der Intelligenz, der sozialen Schicht und sogar früher Rechenfertigkeiten erhalten (Ennemoser et al., in Druck; Krajewski & Schneider, 2009a).
Trainingsstudien zur Förderung mathematischer Basiskompetenzen
Nachdem es inzwischen als belegt gelten kann, dass mathematische Basiskompetenzen im Sinne der oben genannten Zahl-Größen-Kompetenzen einen guten Prädiktor für die spätere Leistungsentwicklung in Mathematik darstellen, bleibt zu prüfen, inwiefern sie tatsächlich auch einen Ansatzpunkt für wirksame Präventionsmaßnahmen bieten. Diesbezüglich findet sich in den letzten Jahren eine stetig wachsende Anzahl an Trainingsstudien, die mehr oder weniger explizit auf eine Förderung mathematischer Basiskompetenzen abzielen. Van Luit und van de Rijt (1998) förderten mit ihrem niederländischen Trainingsprogramm „Additional Early Mathematics“ die Zahl-Größen-Kompetenzen (wie etwa Zahlwortgebrauch, Anzahlseriation oder Anzahlbeziehungen) von vier- bis siebenjährigen Kindern, welche im Bereich dieser Vorläuferfertigkeiten eine ungünstige Ausgangslage aufwiesen. In einem nach Abschluss der Förderung durchgeführten Test zur Zahlbegriffsentwicklung erreichte die Trainingsgruppe das Kompetenzniveau einer altersgleichen Normstichprobe. Die registrierten Verbesserungen im Bereich der Zahl-Größen-Kompetenzen waren über einen Zeitraum von sieben Monaten hinweg stabil. Allerdings wurde nicht untersucht, inwieweit die gefundenen Fördererfolge langfristig auch tatsächlich positive (Transfer-) Effekte auf die schulischen Mathematikleistungen bewirkten.
Die in dieser Untersuchung gefundenen Effekte auf unmittelbar trainierte Basiskompetenzen konnten in einer weiteren Studie von van Luit und Schopman (2000) repliziert werden. Der Transfer auf die Bewältigung nicht trainierter mathematischer Probleme wurde diesmal untersucht, konnte allerdings nicht nachgewiesen werden. Einen möglichen Grund für das Ausbleiben von Transfereffekten sahen die Autoren in mutmaßlich unzureichenden metakognitiven Kompetenzen der Stichprobe, die im Rahmen des Trainings nicht unmittelbar berücksichtigt wurden. Die einbezogene Stichprobe wies neben defizitären Basiskompetenzen auch sprachliche Probleme und Verhaltensauffälligkeiten auf.
Kurzfristige spezifische Trainingseffekte berichten auch Kucian et al. (2011) in ihrer Untersuchung mit schweizerischen 8- bis 10-jährigen Kindern. Eingebettet in ein Computerspiel trainierten sie mit allen teilnehmenden Kindern das räumliche Zuordnen von Zahlen, geschätzten Mengen sowie Additions- und Subtraktionsergebnissen an den Zahlenstrahl bis 100. In einem unmittelbar nach dem Training durchgeführten Nachtest zeigten die Kinder verbesserte Leistungen in den spezifisch trainierten Bereichen. Aufgrund des Versuchsdesigns kann allerdings nicht ausgeschlossen werden, dass es sich hierbei lediglich um natürliche Entwicklungsprozesse oder um Testwiederholungseffekte handelte. Denn zum einen wurden die verbesserten Nachtestleistungen in beiden untersuchten Gruppen (Kinder mit vs. ohne Dyskalkulie) gefunden und zum anderen hatten beide Gruppen dasselbe Training erhalten, d. h. es war keine Kontrollgruppe verfügbar, die eine Evaluation der Trainingseffekte erlauben würde. Langfristige Effekte und Transfereffekte auf nicht explizit trainierte Mathematikleistungen wurden nicht überprüft.
Siegler und Ramani (2008) fanden in ihrer Studie mit amerikanischen Vier- bis Fünfjährigen Trainingseffekte für das so genannte numerical board game. Trainingsinhalt war das Abschreiten und gleichzeitige Aufsagen von Ziffernzahlen (bis 10) auf zehn von links nach rechts angeordneten Feldern. Die auf diese Weise geförderten Kinder erzielten kurzfristig einen höheren Zuwachs in der Lösung von Zahlenstrahlaufgaben als eine Kontrollgruppe, die eine nicht-numerische Version des Trainings erhalten hatte. Whyte und Bull (2008) setzten in ihrer Studie mit schottischen Dreijährigen ebenfalls das numerical board game ein und verglichen die Effekte mit denen zweier Alternativtrainings. Dies war neben einem nicht-numerischen Kontrolltraining eine „nichtlineare“ Variante des board games, welche das Vergleichen, Schätzen und Zuordnen von verschiedenen Äpfelanzahlen zur jeweils zugehörigen verbalen und arabischen Zahl beinhaltete. Beide numerischen Trainings führten im Vergleich mit dem Kontrolltraining zu einer stärkeren kurzfristigen Verbesserung der kindlichen Zähl- und Zahlwortkenntnis sowie auch der Leistungen im Zahlvergleich. Wie in den vorgenannten Studien wurden auch hier weder langfristige Fördereffekte noch Transfereffekte auf die Rechenleistungen der Kinder überprüft.
Link, Moeller, Huber, Fischer & Nuerk (2013) sowie Fischer, Moeller, Bientzle, Cress und Nuerk (2011) berichten schließlich für deutsche Erstklässler beziehungsweise Kindergartenkinder, dass die Einbettung einer räumlichen (Bewegungs-) Komponente in ein mathematisches Training zu besseren Lernerfolgen führt. Allerdings muss einschränkend festgehalten werden, dass diese beiden Studien keinen Rückschluss auf die Wirksamkeit des eigentlichen Mathematiktrainings (ohne zusätzliche Bewegungskomponente) erlauben, da die mathematikspezifischen Trainingsinhalte, ähnlich wie bei Kucian et al. (2011) in allen Versuchsgruppen identisch waren. Da das Studiendesign keine Kontrollgruppe ohne dieses Training beinhaltete, konnten weder der natürliche Entwicklungszuwachs der Kinder noch Messwiederholungseffekte kontrolliert werden. Folglich sind auch keine Aussagen über etwaige Transfereffekte auf schulische Mathematikleistungen möglich. Langfristige Effekte wurden nicht untersucht.
In einer amerikanischen Studie förderten Griffin, Case und Capodilupo (1995) Kleingruppen von Kindergartenkindern mit dem Programm „Number Worlds“. Das Training zielte unter anderem auf Zählfertigkeiten, Übungen zur Identifikation und zum Vergleich von Anzahlen bis hin zu arithmetischen Aufgaben. Ferner wurde im Zuge der Förderung darauf geachtet, dass die Kinder die jeweiligen mathematischen Sachverhalte angemessen sprachlich ausdrücken. Die so trainierten Kinder erreichten im Anschluss an die Förderung bessere Additions- und Subtraktionsleistungen als die Teilnehmer der beiden Kontrollgruppen, die entweder ein phonologisches Training oder aber eine alternative Mathematikförderung erhalten hatten. Längerfristige Transfereffekte auf die schulischen Mathematikleistungen wurden auch in dieser Studie nicht untersucht.
Für den deutschen Raum liegt mit dem Programm „Mengen, zählen, Zahlen“ (MZZ; Krajewski et al., 2007) ein Verfahren vor, das auf dem oben skizzierten entwicklungspsychologischen Modell der Zahl-Größen-Verknüpfung basiert und sehr gezielt auf die Stimulation der in diesem Modell definierten Basiskompetenzen angelegt ist (vgl. Krajewski & Ennemoser, 2013). Im Rahmen des Programms werden schrittweise zunächst numerische Basisfertigkeiten vermittelt (Zählfertigkeiten und Ziffernkenntnis im Zahlenraum bis 10; Ebene 1) und die Kinder zum Verständnis des Anzahlkonzepts hingeführt (Ebene 2), bevor in der dritten Trainingsphase schließlich das Verständnis für Zahlrelationen (Ebene 3) im Mittelpunkt steht. Dies geschieht ausschließlich mit konkret-anschaulichen und bildlichen Materialen; sowohl mathematische Rechenbegriffe wie „plus“, „minus“ oder „ist gleich“ als auch Rechenaufgaben auf Symbolebene (z. B. 1 + 3 = 4) sind explizit nicht Gegenstand der Förderung. Die verwendeten Darstellungsmittel sind so gewählt, dass sie die Struktur der Zahlen an einem äußeren Modell veranschaulichen und zur Modellierung verschiedener quantitativer Aspekte herangezogen werden können. Besonders viel Wert wird darauf gelegt, dass die Kinder die numerischen Beziehungen auch verbalisieren (z. B. „Fünf sind genau eins mehr als vier.“) und über ihre numerischen Handlungen reflektieren.
Eine Reihe von Trainingsstudien liefert Evidenz für die Wirksamkeit des MZZ, wobei sich das ursprünglich für den Einsatz im Kindergarten konzipierte Förderprogramm inzwischen auch in schulischen Lernsettings empirisch bewährt hat (Ennemoser, 2010; Krajewski, Nieding & Schneider, 2008; Ennemoser & Krajewski, 2007; Hasselhorn & Linke-Hasselhorn, 2013). In einer ersten Interventionsstudie konnte gezeigt werden, dass Vorschulkinder nach einer Förderung mit dem MZZ größere Zuwächse in ihren Zahl-Größen-Kompetenzen verzeichnen konnten als Kinder, die ein Denktraining, eine alternative mathematische Förderung oder keine spezielle Förderung erhalten hatten (Krajewski et al., 2008). Die Überlegenheit der MZZ-geförderten Kinder war auch sieben Monate nach Abschluss der Förderung noch nachweisbar. Neben spezifischen Effekten auf die Zahl-Größen-Kompetenzen wurden zwar auch Transfereffekte auf die schulischen Mathematikleistungen registriert. Allerdings waren diese nur im Vergleich zur alternativen mathematischen Förderung statistisch signifikant, nicht gegenüber der Denktrainings-Gruppe oder der untrainierten Kontrollgruppe. Eine mögliche Erklärung für die ausbleibenden Transfereffekte sahen die Autoren im frühen Interventionszeitpunkt während des letzten Kindergartenjahres. So hatte zwischen Trainingsende und Schulbeginn eine Spanne von neun Monaten Wartezeit gelegen, während der die Kinder zunächst gar keine Möglichkeit hatten, das Gelernte direkt auf schulische Inhalte im Mathematikunterricht zu übertragen.
Im Rahmen einer Studie von Ennemoser und Krajewski (2007) wurde das Training erstmals in einem schulischen Lernsetting überprüft. Hierbei wurden zunächst mithilfe des Deutschen Mathematiktests für erste Klassen (DEMAT 1+; Krajewski, Küspert & Schneider, 2002) Risikokinder ausgelesen und anschließend auf zwei Fördergruppen verteilt. Eine Gruppe erhielt zwei Monate vor Ende des ersten Schuljahres eine Förderung mit ausgewählten Sitzungen des MZZ, die andere erhielt zeitgleich eine lesespezifische Förderung. Die MZZ-Gruppe konnte im Verlauf des Trainings signifikant größere Zugewinne in ihren Mathematikleistungen verzeichnen. Die Autoren interpretierten diesen Befund als Evidenz für die oben geäußerte Annahme, dass die Möglichkeit das Gelernte unmittelbar im regulären Mathematikunterricht anzuwenden, einen Transfer auf die Mathematikleistungen in der Schule begünstigt.
Zwei weitere Untersuchungen, in denen das MZZ in Vorklassen1 angewendet wurde, lieferten ebenfalls Hinweise auf die Einsetzbarkeit des Verfahrens im Schulkontext. In einer Studie von Ennemoser (2010) wurden die ersten Stunden des Anfangsunterrichts in Mathematik durch eine MZZ-Förderung ersetzt. Die auf diese Weise in die Mathematik eingeführten Kinder konnten im Trainingszeitraum deutlich größere Zugewinne im Bereich ihrer Zahl-Größen-Kompetenzen verzeichnen als Kinder, die dem konventionellen Vorklassenunterricht in Mathematik gefolgt waren. Hasselhorn und Linke-Hasselhorn (2013) setzten das Training ebenfalls in Vorklassen ein, hier jedoch in Form einer Kleingruppenförderung, und ermittelten beachtliche Effektstärken zugunsten der MZZ-geförderten Kinder. Allerdings beschränken sich beide Studien auf die Analyse kurzfristiger Effekte. Der Transfer auf die nachfolgenden Schulleistungen in Mathematik wurde nicht überprüft.
Schließlich wurde die Wirksamkeit des MZZ über den Einsatz im Kindergarten und im Regelschulbereich hinausgehend inzwischen auch mit ermutigenden Befunden in sonderpädagogischen Lernsettings evaluiert (Lernhilfeschule: Sinner & Kuhl, 2010; Schule für Geistig Behinderte: Kuhl, Sinner & Ennemoser, 2012).
Zusammenfassend lässt sich festhalten, dass die bislang publizierten Evaluationsstudien einerseits vergleichsweise konsistente Belege für die Förderpotenziale des MZZ liefern. Andererseits beschränken sich die Studien in der Mehrzahl auf die Überprüfung kurzfristiger Effekte. Zudem wurde nicht durchgängig überprüft, inwieweit die gefundenen Fördererfolge auch tatsächlich auf die eigentlich im Zentrum des Interesses stehenden Mathematikleistungen in der Schule transferieren.
Ziele der Untersuchung
Im Rahmen der vorliegenden Studie sollte die Wirksamkeit des MZZ-Trainings bei zuvor identifizierten Erstklässlern mit dem Risiko einer drohenden Rechenschwäche untersucht werden. Dabei wurde angenommen, dass das Training sowohl kurzfristige, d. h. unmittelbar nach Abschluss der Förderung messbare, als auch langfristige Effekte auf die Entwicklung der Zahl-Größen-Kompetenzen hat. Ferner wurde erwartet, dass diese Zugewinne im Bereich der Zahl-Größen-Kompetenzen auch tatsächlich in erwarteter Weise auf die nachfolgende Entwicklung von Rechenfertigkeiten transferieren.
Methodik
Stichprobe, Untersuchungsdesign und Förderverfahren
Die vorliegende Fragestellung wurde mit einem 2-Gruppen-Prätest-Posttest-Follow-up-Design untersucht. 238 Erstklässler (127 Jungen, 111 Mädchen) aus insgesamt 13 deutschen Schulklassen nahmen vier Monate nach Schuleintritt (Dezember) an einem Screening zur Erfassung von Zahl-Größen-Kompetenzen teil. Anhand der hierbei gezeigten Leistungen wurden 66 Kinder, deren Leistung unterhalb eines Prozentrangs von 25 lag, als Risikokinder klassifiziert (vgl. Ennemoser et al., in Druck) und auf Klassenebene randomisiert auf zwei Versuchsbedingungen aufgeteilt (Fördergruppe und Kontrollgruppe). 64 der auf diese Weise identifizierten Risikokinder nahmen an allen drei Messzeitpunkten teil, zwei Kinder schieden wegen Umzug oder Krankheit aus. So verblieben in jeder der beiden Versuchsgruppen 32 Kinder (jeweils 16 Mädchen und 16 Jungen).
Die Fördergruppe arbeitete anschließend über einen Zeitraum von fünf Wochen je zwei Schulstunden wöchentlich mit ausgewählten Sitzungen des Programms „Mengen, zählen, Zahlen“ (Krajewski et al., 2007). Im Rahmen des Programms werden ausschließlich Basiskompetenzen im Sinne des oben beschriebenen Entwicklungsmodells gefördert. Explizit nicht Bestandteil der Förderung sind konventionelle Rechenaufgaben. Diese werden weder in sprachlicher Form (z. B. keine Verwendung der Begriffe „plus“ und „minus“) noch in symbolischer Form (keine Verwendung von Operatoren bzw. Verhältniszeichen +, −, =, <, >) behandelt.
Das in der Originalfassung 24 Sitzungen zu je 30 Minuten umfassende Trainingsprogramm wurde für die Anwendung im Schulkontext angepasst. So wurden die ersten fünf Sitzungen zur Vermittlung der Ziffernkenntnis (Ebene 1) ausgespart, da nach einem halben Jahr Mathematikunterricht entsprechende Kenntnisse auch bei schwächeren Schülern weitestgehend vorausgesetzt werden konnten (Ennemoser et al., in Druck). Pilotierend durchgeführte Fördersitzungen hatten ergeben, dass im Vergleich zur Anwendung im Kindergarten mit einer reduzierten Durchführungsdauer pro Übungseinheit gerechnet werden konnte. Aus diesem Grunde konnten die verbleibenden 19 Sitzungen zu den Kompetenzebenen 2 und 3 auf insgesamt zehn Sitzungen komprimiert werden. Das Training wurde von Lehramtsstudierenden in Gruppen mit drei bis sieben Schülern durchgeführt. Die Gruppengröße ergab sich jeweils aus der Anzahl von Kindern, die innerhalb einer Klasse als förderbedürftig klassifiziert worden waren. Im Verlauf der Fördersitzungen bearbeiteten die Kinder zunächst Einheiten zum präzisen Anzahlkonzept. Anschließend beschäftigten sie sich mit der Zusammensetzung und Zerlegung von Zahlen sowie mit Differenzen zwischen (An-)Zahlen. Die Kontrollgruppe erhielt kein spezielles Training. Stattdessen nahmen die betreffenden Kinder nach Rückmeldung der Vortestergebnisse an konventionellen Förderstunden der jeweiligen Schule teil. Nach Abschluss des Trainings wurden im März erneut die Zahl-Größen-Kompetenzen der teilnehmenden Kinder erhoben (Nachtest). Um die Stabilität der Effekte zu überprüfen, folgte kurz vor Ende des Schuljahres eine dritte Erhebung (Juni, Follow-up).
Testverfahren
Zur Erfassung der Zahl-Größen-Kompetenzen im ersten Schulhalbjahr und zur Identifikation der Risikokinder wurde eine Vorversion des Gruppentests „Mathematische Basiskompetenzen ab Schuleintritt“ (MBK 1+; Ennemoser et al., in Druck) herangezogen. Die Kompetenzen auf Ebene 1 wurden durch zwei Subtests erfasst. Beim Zahlendiktat wurden zehn Zahlen in den Zahlenräumen bis 10 (2 Items), 20 (5 Items) und 100 (3 Items) diktiert. Für jede korrekt verschriftliche Zahl wurde ein halber Punkt vergeben, so dass insgesamt 5 Punkte erreicht werden konnten. Im Untertest Zahlenlücken wurden jeweils zwei Zahlen präsentiert und die Aufgabe bestand darin, die genau zwischen diesen beiden Zahlen liegende Zahl einzutragen (4 Items). Wie bei sämtlichen nachfolgend beschriebenen Aufgaben wurde jede korrekte Antwort mit einem Punkt bewertet. Somit konnten hier maximal 4 Punkte erzielt werden.
Kompetenzen auf der Ebene 2 wurden mithilfe von vier Aufgabentypen erfasst. Der Subtest Anzahlkonzept umfasste zwei Items, bei denen jeweils eine vorgegebene Anzahl von Objekten der zugehörigen Ziffer zugeordnet werden musste. In der Zahlenstrahlaufgabe mussten Zahlen an einem Zahlenstrahl lokalisiert bzw. an der entsprechenden Position handschriftlich eingetragen werden (5 Items). Beim anschließend zu bearbeitenden Subtest Zahlvergleiche wurden jeweils zwei Zahlen vorgegeben. Durch Angabe der Relationszeichen (<, >, =) musste entschieden werden, welche Zahl größer oder kleiner ist bzw. ob beide Zahlen gleich groß sind (4 Items). Um sicherzustellen, dass die Relationszeichen bekannt sind, wurden diese vorher explizit erläutert. Bei den Aufgaben zur Anzahlseriation musste in eine unvollständige Kärtchenreihe, auf der eine ansteigende Anzahl von Objekten zu sehen war, das jeweils fehlende Kärtchen korrekt eingeordnet werden (3 Items).
Drei Subtests dienten zur Erfassung der Kompetenzen auf Ebene 3. In den Aufgaben zum Teil-Ganzes-Verständnis wurden links und rechts von einem Gleichheitszeichen Dominosteine dargestellt, wobei eines der vier Punktefelder frei blieb. Auf diesem Feld musste jene Anzahl von Punkten ergänzt werden, die erforderlich war, damit auf beiden Dominosteinen dieselbe Gesamtpunktzahl resultierte (4 Items). Der Subtest Zahlzerlegung bestand aus vier Platzhalteraufgaben, die nun bereits auf symbolischer Ebene zu lösen waren (z. B. 3 + __ = 5). Darüber hinaus wurden vier Textaufgaben vorgegeben, die das Verständnis für die Beziehungen zwischen Zahlen erfassten und im Testheft bildlich veranschaulicht waren. Insgesamt konnten maximal 35 Punkte erreicht werden.
Um mögliche Transfereffekte zu erfassen, wurden zusätzlich zum Test mathematischer Basiskompetenzen zu jedem Messzeitpunkt auch die Rechenleistungen der Kinder überprüft. Im Rahmen der Vortesterhebungen hatten die Kinder je 80 Sekunden Zeit, um möglichst viele von 20 vorgegebenen Additionsaufgaben beziehungsweise zehn Subtraktionsaufgaben (jeweils im Zahlenraum bis 10) zu lösen. Für den Nachtest und die Follow-up-Erhebung wurden die Testzeiten für die beiden Aufgaben aufgrund der rasanten Entwicklungsfortschritte im Verlauf des ersten Schuljahres auf je 40 Sekunden verkürzt. Als abhängige Variable diente jeweils die Anzahl korrekt gelöster Aufgaben (Summe aus Addition und Subtraktion) pro Minute, so dass die Leistungen über die Testzeitpunkte hinweg direkt vergleichbar waren. Ergänzend wurde einmalig als Kontrollvariable die nonverbale Intelligenz mit der Kurzform des CFT 1 (Cattell, Weiß & Osterland, 1997) erhoben.
Ergebnisse
Prüfung auf Unterschiede in den Ausgangsleistungen
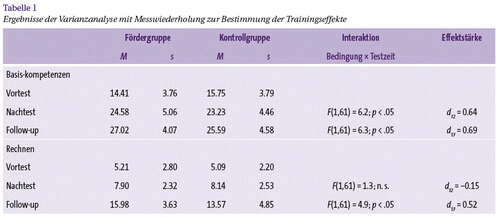
In einem ersten Schritt wurde überprüft, ob sich die beiden Versuchsgruppen bereits zum Vortest in relevanten Merkmalen unterscheiden. t-Tests für unabhängige Stichproben ergaben weder im Bereich der Zahl-Größen-Kompetenzen (t[62] = 1.4, p = .16) noch bei den Rechenfertigkeiten (t[62] = −.21, p = .84) Hinweise auf signifikante Ausgangsunterschiede (vgl. Tab. 1). Auch in Bezug auf das Intelligenzniveau ließen sich keine statistisch bedeutsamen Abweichungen feststellen (t[62] = 1.6, p = .12). Die im CFT 1 durchschnittlich erreichte Punktzahl von 22.03 (s = 4.4) in der Kontrollgruppe bzw. 19.81 (s = 6.7) in der Experimentalgruppe entspricht einem durchschnittlichen IQ von 100 bzw. 96. Die Geschlechterverteilung war in beiden Gruppen identisch.
Überprüfung kurzfristiger Effekte
Zur Überprüfung kurzfristiger Trainingseffekte auf die unmittelbar geförderten Zahl-Größen-Kompetenzen sowie auf die nicht trainierten Rechenfertigkeiten (inhaltlicher Transfer) wurden Varianzanalysen mit Messwiederholung durchgeführt. In das Modell ging jeweils neben dem Faktor Versuchsbedingung die Intelligenz als Kovariate ein. In Bezug auf die Zahl-Größen-Kompetenzen bestätigte sich zunächst ein signifikanter Haupteffekt des Testzeitpunkts (F[1,61] = 8.7, p < .01), das heißt die Kinder konnten im Untersuchungszeitraum bedeutsame Zugewinne in ihren Zahl-Größen-Kompetenzen verzeichnen. Ein signifikanter Haupteffekt der Intelligenz bestätigt zudem, dass Kinder mit besseren intellektuellen Ausgangsleistungen auch über bessere Zahl-Größen-Kompetenzen verfügten (F[1,61] = 4.3, p < .05). Der Haupteffekt der Versuchsbedingung war nicht signifikant (F[1,61] = 0.16, p = .69). Jedoch erwiesen sich die numerisch höheren Zugewinne der MZZ-geförderten Kinder gegenüber der Kontrollgruppe als statistisch bedeutsam (Interaktion Versuchsbedingung × Testzeitpunkt: F[1,61] = 6.2, p < .05; vgl. Abb. 1, Vortest-Nachtest). Dieser Effekt deutet darauf hin, dass das Training kurzfristig wirksam ist. Die um Vortestunterschiede korrigierte Effektstärke nach Cohen (1988) betrug d = 0.64, was als mittlerer Effekt zu interpretieren ist (vgl. Tab. 1). Die Interaktion zwischen Intelligenz und Testzeitpunkt war nicht signifikant (F[1,61] = 1.10, p = .30), das heißt, die im Untersuchungszeitraum erzielten Entwicklungsfortschritte waren nicht vom Intelligenzniveau der Kinder abhängig. 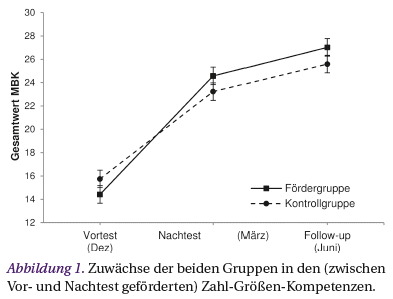
Ein anderes Bild ergab sich mit Blick auf die Rechenfertigkeiten der Kinder. Hier wurde neben dem Haupteffekt der Zeit (F[1,61] = 25.4, p < .01) zwar nicht der Haupteffekt der Intelligenz (F[1,61] = 1.84, p = .18), aber die Interaktion zwischen Intelligenz und Testzeitpunkt signifikant (F[1,61] = 5.2, p < .05). Demnach wurden die zwischen Vor- und Nachtest erzielten Fortschritte in den Rechenfertigkeiten durch die Intelligenz moderiert, wobei Kinder mit guter intellektueller Ausgangslage größere Zuwächse verzeichnen konnten als weniger intelligente Kinder. Ein Einfluss der Versuchsbedingung zeigte sich in diesem Zeitraum hingegen noch nicht. Weder der entsprechende Haupteffekt (F[1,61] = 0.03, p = .87) noch die Interaktion mit der Zeit wurde statistisch signifikant (F[1,61] = 1.32, p = .26; vgl. Abb. 2, Vortest-Nachtest). 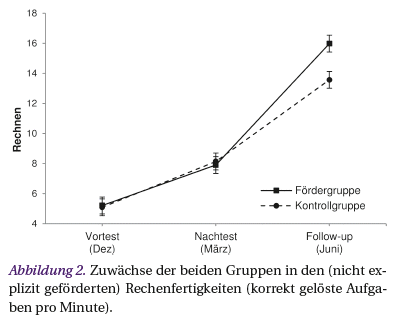
Überprüfung langfristiger Effekte
Zur Überprüfung langfristiger Effekte wurden erneut Varianzanalysen mit Messwiederholung durchgeführt. Die einzige Änderung bestand darin, dass als Wiederholungsmessung nun nicht die Nachtestleistung diente, sondern jeweils die Leistung zur drei Monate später durchgeführten Follow-up-Erhebung. In Bezug auf die Zahl-Größen-Kompetenzen wurden ähnlich wie zuvor signifikante Haupteffekte des Testzeitpunkts und der Intelligenz registriert (F[1,61] = 6.3, p < .05 bzw. F[1,61] = 4.5, p < .05), wohingegen die Interaktion zwischen Intelligenz und Testzeitpunkt statistisch nicht bedeutsam war (F[1,61] = 0.70, p = .41). Während der Haupteffekt der Versuchsbedingung ebenfalls nicht signifikant war (F[1,61] = 0.21, p = .65), ergab sich erneut eine signifikante Interaktion zwischen Versuchsbedingung und Zeit (F[1,61] = 6.3, p < .05). Dies bestätigt auch für den Zeitraum zwischen Vortest und Follow-up-Erhebung signifikant stärkere Zuwächse der MZZ-geförderten Kinder im Bereich ihrer Zahl-Größen-Kompetenzen (vgl. Abb. 1, Vortest-Follow-up). Die Effektstärke lag mit d = .69 in derselben Größenordnung wie zuvor.
Bezüglich der Rechenleistungen der Kinder ergab sich für das Follow-up ein anderes Bild als zum Nachtest. Neben dem signifikanten Haupteffekt des Testzeitpunkts (F[1,61] = 29.9, p < .01) war hier weder der Haupteffekt der Intelligenz noch die Interaktion zwischen Intelligenz und Testzeitpunkt statistisch bedeutsam (F[1,61] = 2.55, p = .12 bzw. F[1,61] = 0.17, p = .70). Anders als unmittelbar nach Abschluss der Förderung ergab sich nun aber ein signifikanter Haupteffekt der Versuchsbedingung (F[1,61] = 4.1, p < .05), der zudem durch eine Interaktion mit dem Testzeitpunkt moderiert wurde (F[1,61] = 4.9, p < .05). Die MZZ-Förderung ging also – langfristig betrachtet – mit höheren Leistungen in den (nicht trainierten) Rechenfertigkeiten einher (vgl. Abb. 2, Vortest-Follow-up). Die um Vortestunterschiede korrigierte Effektstärke betrug d = 0.52 und lag damit in einer mittleren Größenordnung.
Pfadmodell zur Überprüfung der Transfereffekte (Mediatoranalyse)
Um zu überprüfen, ob die langfristig höheren Zuwächse der Förderkinder in den Rechenfertigkeiten tatsächlich auf die durch das Training gesteigerten Zahl-Größen-Kompetenzen zurückzuführen sind, wurde ein Pfadmodell aufgestellt und mit den vorliegenden Daten empirisch überprüft (Abb. 3). Zunächst zeigten sich, wie nicht anders zu erwarten, signifikante Einflüsse der Vortestleistungen auf die jeweils nachfolgenden Leistungen im Nachtest beziehungsweise im Follow-up. Die autoregressiven Effekte zwischen den beiden Wiederholungsmessungen lagen zwar mit β = .44 (p < .01) für die Zahl-Größen-Kompetenzen sowie β = .32 (p < .01) für die Rechenfertigkeit etwas niedriger als für die hier verwendeten Testverfahren üblicherweise berichtet (vgl. Ennemoser et al., in Druck). Da es sich bei der Stichprobe jedoch um Risikokinder handelt, die in den beiden Verfahren homogen schwache Leistungen erbracht haben, ist die Leistungsvarianz insgesamt deutlich eingeschränkt, so dass von vornherein mit etwas geringeren Retest-Korrelationen zu rechnen war. 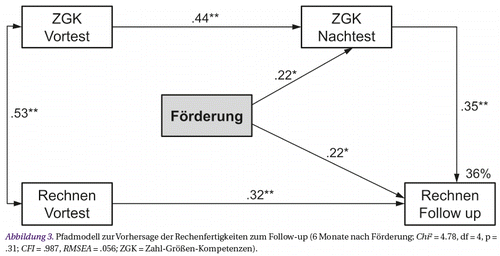
Wie aufgrund der bereits durchgeführten Varianzanalysen ebenfalls zu erwarten, ließ sich darüber hinaus ein förderlicher Effekt der MZZ-Förderung auf die Zahl-Größen-Kompetenzen im Nachtest statistisch absichern (β = .22, p < .05; Kodierung MZZ = 1; Kontrollgruppe = 0). Die Förderung bewirkte demnach spezifische Effekte auf die unmittelbar trainierten Kompetenzen. Darüber hinaus fand die Annahme, dass die (zeitverzögerten) Transfereffekte auf die Rechenperformanz durch vorangegangene, trainingsbedingte Zuwächse in den Zahl-Größen-Kompetenzen mediiert werden, nur teilweise Unterstützung. Zwar ergab sich der erwartete Effekt der im Nachtest erfassten Zahl-Größen-Kompetenzen auf die Rechenleistungen im Follow-up Test (β = .35, p < .01) und damit ein indirekter Trainingseffekt auf Rechenfertigkeiten, der theoriekonform über Zahl-Größen-Kompetenzen vermittelt wurde. Allerdings blieb nach Kontrolle dieses indirekten Pfades auch der direkte Trainingseffekt auf die Rechenfertigkeiten der Kinder statistisch signifikant (β = .22, p < .05). Eine Nullsetzung dieses Pfads führte zu einer signifikanten Verschlechterung des Modells (Chi2 = 4.47, df = 1, p < .05) und bestätigte damit die Relevanz des „direkten“ Effektes. Es ist demnach naheliegend, dass die langfristigen Vorteile der MZZ-geförderten Kinder gegenüber der Kontrollgruppe auch noch durch weitere, nicht im Modell enthaltene Mediatorvariablen vermittelt wurden.
Diskussion
Anhebung der Zahl-Größen-Kompetenzen als langfristiger Motor der Rechenentwicklung
Als zentrales Ergebnis der Studie ist festzuhalten, dass die mathematische Entwicklung von Erstklässlern, die von einer Rechenschwäche bedroht sind, wirksam unterstützt werden kann. Eine entwicklungsorientierte Förderung mit dem Programm „Mengen, zählen, Zahlen“ (MZZ; Krajewski et al., 2007) konnte nicht nur Lücken in den mathematischen Basiskompetenzen der Kinder kurz- und langfristig schließen. Die Förderung schlug sich langfristig auch in gesteigerten Rechenfertigkeiten der Kinder nieder. Da die Bearbeitung konventioneller Rechenaufgaben auf Symbolebene kein Gegenstand der Förderung war, handelt es sich hierbei um einen Transfereffekt. Der Befund, dass dieser Effekt erst mit einer zeitlichen Verzögerung auftrat, deutet darauf hin, dass mithilfe des Trainings erfolgreich Entwicklungslücken auf Ebene der Basiskompetenzen geschlossen werden konnten, so dass im Anschluss die Inhalte des regulären Unterrichts auch ohne weitere Förderung auf einen fruchtbareren Boden fallen konnten. Diese Interpretation wird auch durch die Ergebnisse der Pfadanalyse gestützt, die darauf hindeuten, dass der zeitverzögerte Transfereffekt – zumindest teilweise – durch die zuvor angehobenen Zahl-Größen-Kompetenzen vermittelt wurde. Allerdings handelt es sich hierbei nicht um eine vollständige Mediation, da neben dem indirekten Trainingseffekt über die Zahl-Größen-Kompetenzen auch der „direkte“ Trainingseffekt auf die drei Monate später erfassten Rechenfertigkeiten statistisch signifikant blieb. Da Rechenfertigkeiten in der MZZ-Förderung jedoch nicht direkt trainiert wurden, ist es naheliegend, dass hier weitere vermittelnde Variablen involviert waren, die in der vorliegenden Studie lediglich nicht erfasst wurden. Hierfür kommen insbesondere motivationale Faktoren in Frage. So ist es denkbar, dass die Risikokinder aufgrund ihrer schlechten Ausgangslage bereits zu diesem Zeitpunkt die eigenen Schwierigkeiten im Mathematikunterricht registriert hatten, was gegebenenfalls in einer schlechteren Einstellung, der Ausbildung eines negativen Selbstkonzepts sowie geringeren Erfolgs- und Selbstwirksamkeitserwartungen münden und auf diesem Wege einen abträglichen Einfluss auf die weitere Leistungsentwicklung nehmen kann. Die MZZ-Förderung könnte einer solchen ungünstigen Entwicklung entgegengewirkt haben, indem sie nicht direkt an bereits überfordernden Rechenaufgaben ansetzte, sondern an den für deren Lösung erforderlichen Zahl-Größen-Kompetenzen, welche bei den Risikokindern möglicherweise gerade in der Zone der nächsten Entwicklung lagen (Vygotskij, 1978).
Eine weitere Erklärung für den verbleibenden (vermutlich nicht wirklich „direkten“) Effekt könnte darin liegen, dass die Schüler durch die Förderung langfristig eine verbesserte mentale Zahlenrepräsentation aufbauen, die nicht nur dem besseren Verständnis für die Beziehungen zwischen Zahlen dienlich ist (verbessertes Zahl-Größen-Verständnis), sondern die es zudem – auch beim Rechnen auf Symbolebene – ermöglicht, immer effizienter und zunehmend automatisiert auf die im Langzeitgedächtnis abgelegten Größenrepräsentationen zuzugreifen (ähnlich dem „Sicht-Wortschatz“ im Schriftsprachbereich).
Entwicklungsorientierte Kompetenzförderung statt Performanzorientierung
Insgesamt liefern die Befunde Evidenz für die Wirksamkeit von Maßnahmen, die sich explizit an theoretischen Modellierungen der Kompetenzentwicklung orientieren. Im Umkehrschluss sprechen sie somit auch für die Bedeutsamkeit und für die Gültigkeit aktueller Entwicklungsmodelle (in diesem Falle des ZGV-Modells), die deshalb in der täglichen pädagogischen Praxis und in spezifischen mathematischen Fördermaßnahmen größere Aufmerksamkeit erhalten sollten. Außerdem verleihen die Ergebnisse Forderungen Nachdruck, die eine Verschiebung weg von einer performanzorientierten Förderung (die primär auf die Produktion richtiger Lösungen fokussiert) in Richtung einer verständnisorientierten Kompetenzvermittlung, verlangen. Eine solche Förderung schließt nicht nur Entwicklungslücken, sondern sie bewirkt auch ein besseres Verständnis für die abstrakten mathematischen Zusammenhänge und hebt insgesamt das Kompetenzniveau, wovon die Kinder später beim Rechnen profitieren können, wie diese Studie belegt.
Die Frage nach dem optimalen Förderzeitpunkt
Die vorliegende Untersuchung zeigt abermals, dass das eigentlich für den Vorschulbereich konzipierte Förderprogramm MZZ auch nach dem Schuleintritt noch eine wirksame Präventionsmaßnahme darstellt. Dies gilt zumindest für die hier im Blickpunkt stehende Zielgruppe von Kindern, die ein erhöhtes Risiko für die Entstehung einer Rechenschwäche aufweisen. Die Befunde stützen gar die eingangs geäußerte Annahme, dass der Einsatz nach dem Schuleintritt noch Erfolg versprechender ist als ein Einsatz im Kindergarten, weil die Kinder die Möglichkeit haben, die neu erworbenen (Basis-)Kompetenzen unmittelbar auf die Anforderungen im regulären Unterricht zu übertragen. So zog nach den Befunden von Krajewski et al. (2008) eine MZZ-Förderung sechs Monate vor der Einschulung zwar positive Effekte auf die Zahl-Größen-Kompetenzen nach sich; ein Transfer auf die späteren Schulleistungen in Mathematik war beim Vergleich mit einem allgemeinen kognitiven Training jedoch nicht nachweisbar. Ennemoser und Krajewski (2007) fanden hingegen bei einem Einsatz im ersten Schuljahr bereits unmittelbar nach dem Training einen signifikanten Transfereffekt auf die schulischen Mathematikleistungen.
Gleichwohl kann die Frage nach dem optimalen Förderzeitpunkt anhand der vorliegenden Studien nicht zufriedenstellend beantwortet werden. Denn während in der Kindergartenstudie unselektierte Gruppen gefördert wurden (im Sinne einer primärpräventiven Maßnahme), wurde das Programm im Schulkontext gezielt mit zuvor per Screening ausgelesenen oder aber in Vorklassen befindlichen Risikokindern durchgeführt (im Sinne einer sekundärpräventiven Maßnahme). Es ist durchaus denkbar, dass die in Bezug auf Transfereffekte abweichenden Befunde dahingehend zu interpretieren sind, dass die Potenziale des MZZ-Trainings eher im Bereich der Sekundärprävention liegen, wonach nur für Kinder mit einer schwachen Ausgangslage Transfereffekte auf mathematische Schulleistungen zu erwarten wären. Dem widersprechen allerdings die Befunde einer aktuellen, groß angelegten Trainingsstudie, in welcher der Anfangsunterricht in Mathematik durch eine MZZ-angelehnte Förderung ersetzt wurde (Ennemoser, Krajewski, Vossen & Haschke, 2013). Hier deuten erste Befunde darauf hin, dass eine strikt entwicklungsorientierte Förderung von Zahl-Größen-Kompetenzen auch klassenintegriert durchführbar ist und darüber hinaus unabhängig vom Risikostatus der betreffenden Kinder langfristige Transfereffekte auf die mathematischen Schulleistungen haben kann. Allerdings scheint es für eine unterrichtsintegrierte Anwendung (mit unausgelesenen Stichproben) von zentraler Bedeutung zu sein, dass die Basiskompetenzförderung unmittelbar nach Schuleintritt beginnt. Völker, Otto, Fauth, Krajewski und Büttner (2014) berichten, dass eine erst Mitte des Schuljahres (ebenfalls unterrichtsintegriert) durchgeführte MZZ-Förderung, hier allerdings gekoppelt mit einem Selbstregulationstraining, keine Effekte auf die Zahl-Größen-Kompetenzen erzielte. Speziell für die beteiligten Risikokinder wurden zwar kurzfristige Effekte auf die Rechenleistungen registriert, diese hatten jedoch nicht langfristig Bestand.
Auch wenn die Frage nach dem optimalen Förderzeitpunkt (Kindergarten vs. direkt nach Schuleintritt) noch nicht abschließend beantwortet werden kann, zeigen die Befunde der vorliegenden, sowie auch die Ergebnisse weiterer aktueller Studien, dass eine entwicklungsorientierte Förderung von Zahl-Größen-Kompetenzen einen außerordentlich effektiven Präventionsansatz darstellt. In der Tendenz deuten die bislang vorliegenden Befunde darauf hin, dass eine unterrichtsintegrierte Förderung (für alle Kinder) direkt im Anfangsunterricht stattfinden sollte, weil hierbei sehr basale Inhalte fokussiert werden, die im herkömmlichen Curriculum keine hinreichende Beachtung finden. Es handelt sich somit um Maßnahmen, die geeignet sind, um der Entstehung von Entwicklungslücken vorzubeugen (Primärprävention). Demgegenüber ist eine Kleingruppenförderung mit Risikokindern auch einige Monate nach dem Schuleintritt noch wirksam, wobei in diesem Falle bereits vorhandene Entwicklungslücken geschlossen werden können (Sekundärprävention).
Grenzen der vorliegenden Untersuchung
Ungeachtet der ermutigenden Ergebnisse sollte nicht unerwähnt bleiben, dass die vorliegende Studie auch einige Grenzen aufweist, die bei der Interpretation der Befunde zu berücksichtigen sind. Zum einen lag der Untersuchung eine vergleichsweise kleine Stichprobe zugrunde. Größere Stichproben sind bei Studien mit ausgelesenen Risikokindern naturgemäß schwieriger zu realisieren als bei unausgelesenen Stichproben, und die vorliegenden Versuchspersonenzahlen liegen sicher in einer durchaus aussagekräftigen Größenordnung. Dennoch machen es die vergleichsweise kleinen Fallzahlen zwingend erforderlich die Gültigkeit der jeweiligen Befunde durch Replikationsstudien abzusichern. Unter Rückgriff auf größere Stichproben könnten zudem auch differenziertere Fragestellungen inferenzstatistisch überprüft werden als dies in der vorliegenden Studie möglich war. Hierzu zählt beispielsweise die Frage, ob die Größe der Fördergruppe einen moderierenden Einfluss auf die Trainingszugewinne hat.
Ferner wurde die Mathematikleistung in der vorliegenden Untersuchung lediglich durch die Rechenfertigkeit, genauer gesagt, durch die Effizienz beim Lösen einfacher Rechenaufgaben operationalisiert. Aussagekräftiger wäre sicher die Durchführung eines standardisierten, curricular validen Testverfahrens, in dem ein repräsentativer Ausschnitt der Unterrichtsanforderungen im mathematischen Anfangsunterricht abgeprüft wird. Darüber hinaus wurde nicht systematisch kontrolliert, welche konkreten Fördermaßnahmen die Kinder der Kontrollgruppe erhielten. Dies stellt zweifellos eine der zentralen Schwächen der vorliegenden Studie dar. Genaue Informationen über die jeweils im Förderunterricht behandelten Inhalte würden sicher differenziertere Aussagen über die Wirksamkeit bzw. die relative Wirkungslosigkeit der üblicherweise ergriffenen Maßnahmen ermöglichen. Zudem kann nicht ausgeschlossen werden, dass bestimmte Besonderheiten der Fördersituation, insbesondere die Durchführung der Fördermaßnahmen durch externe Trainer, nicht doch auch Zuwendungseffekte verursacht hat, die für den größeren Lernerfolg der MZZ-geförderten Kinder mit verantwortlich sind. Hier sollten zukünftige Studien trainierte Kontrollgruppen etablieren, die ebenfalls von externen Förderkräften angeleitet werden. Alternativ könnten auch alle beteiligten Versuchsgruppen durch das reguläre Lehrpersonal der Schule gefördert werden. Letzteres würde auch Rückschlüsse auf die Implementierbarkeit der Maßnahmen in die Praxis beziehungsweise über die Wirksamkeit der MZZ-Förderung unter alltagspraktischen Bedingungen in der Schule erlauben.
Abschließend sei darauf hingewiesen, dass die vorliegenden Befunde bereits vor ihrer Publikation Eingang in eine Meta-Analyse von Ise, Dolle, Pixner und Schulte-Körne (2012) gefunden haben, wobei die hier berichteten zentralen Ergebnisse durch die dort gewählte Auswertungsstrategie nicht angemessen dokumentiert werden. So verzichteten die Autoren in ihrer Analyse darauf, (signifikante) langfristige Effekte überhaupt in die vergleichende Studienübersicht einzubeziehen, weil diese in den aufgenommenen Untersuchungen üblicherweise nicht überprüft wurden. Darüber hinaus wurden kurzfristige spezifische Effekte auf gegebenenfalls trainierte (Basis-) Kompetenzen nur dann in die Gesamtbewertung einbezogen, wenn zeitgleich keine zusätzliche Überprüfung des Transfers auf mathematische Schulleistungen stattgefunden hatte (weil ja Transfermaße für die Rechenleistung vorhanden waren). In der Konsequenz bilanziert die Meta-Analyse für die vorliegende Studie lediglich einen kurzfristigen Nulleffekt auf Rechenleistungen, während die wichtigsten Befunde unberücksichtigt bleiben. Dies sind zum einen die theoretisch überaus plausiblen, erst zeitverzögert auftretenden, langfristigen Transfereffekte auf Rechenleistungen und zum anderen die – sowohl kurz- als auch langfristig gefundenen – spezifischen Effekte auf die mathematischen Basiskompetenzen.
Implikationen für die Praxis
Die vorgelegte Studie befasst sich mit Möglichkeiten der Prävention von Rechenschwierigkeiten. Für die Praxis der Lernförderung – insbesondere im schulischen Kontext – lassen sich aus der theoretischen Grundlegung, der methodischen Vorgehensweise sowie den resultierenden Befunden drei wesentliche Implikationen ableiten. (1) Die Studie unterstreicht die Bedeutung früh erworbener, mathematikspezifischer Voraussetzungen, die für den erfolgreichen Einstieg in die Schulmathematik erforderlich sind und lokalisiert in diesem Bereich auch das „Kerndefizit“ von Rechenschwierigkeiten. (2) Sie weist auf inzwischen verfügbare diagnostische Möglichkeiten zur Früherkennung ungünstiger Entwicklungsverläufe hin. (3) Die Studie zeigt insbesondere, auf welche Weise drohenden Fehlentwicklungen bereits kurz nach dem Schuleintritt effektiv – und mit einem relativ überschaubaren Aufwand – entgegengewirkt werden kann. Diese Implikationen werden im Folgenden näher ausgeführt.
(1) Lokalisieren der Ursachen für ungünstige Entwicklungsverläufe
Obwohl die schulische Leistungsentwicklung im Fach Mathematik von vielen verschiedenen Faktoren beeinflusst wird, spielen so genannte „mathematische Basiskompetenzen“ zweifellos die wichtigste Rolle. Mathematische Basiskompetenzen stellen im Sinne einer Vorläuferfertigkeit eine wichtige Voraussetzung dar, um für die Anforderungen im mathematischen Anfangsunterricht hinreichend gewappnet zu sein. Aktuelle Entwicklungsmodelle zeigen auf, welche Entwicklungsschritte vollzogen werden müssen, damit einfache Rechenaufgaben im Mathematikunterricht kompetent gelöst werden können. Das dieser Arbeit zugrunde gelegte Modell der Zahl-Größen-Verknüpfung (Krajewski, 2007) richtet den Fokus besonders auf solche „Meilensteine“ in der mathematischen Kompetenzentwicklung, deren Bedeutung in der Praxis häufig übersehen wird, weil sie dem kompetenten Rechner (irrtümlicherweise) als trivial erscheinen, so dass sie letztendlich nicht hinreichend gefördert werden. Von zentraler Bedeutung sind vor allem jene Entwicklungsschritte, die zwischen dem Kennenlernen von Zahlwörtern einerseits und dem kompetenten Lösen von symbolisch dargestellten Rechenaufgaben andererseits liegen. Diese beinhalten ein vertieftes Verständnis für die Verknüpfung von Zahlen mit Größen. Zwar begreifen die meisten Kinder recht schnell, dass Zahlen „irgendwie“ mit Mengen und Größen zu tun haben. Um aber mit Zahlen kompetent operieren zu können, müssen Kinder verstehen, dass ein bestimmtes Zahlwort oder eine bestimmte Ziffer immer eine exakt festgelegte Anzahl oder Größe repräsentiert. Zudem ist das Verständnis erforderlich, dass sich Anzahlen zerlegen und wieder zusammenfügen lassen und dass der Unterschied zwischen zwei Zahlen wiederum exakt mit einer bestimmten Zahl beschrieben werden kann. Dass Rückstände im Erwerb dieser Basiskompetenzen ein „Kerndefizit“ der Rechenschwäche darstellen, lässt sich inzwischen aus zahlreichen, auch neuropsychologischen Befunden ableiten (vgl. Krajewski & Ennemoser, 2013).
(2) Möglichkeiten der Früherkennung
Die Kenntnis relevanter Basiskompetenzen macht es möglich, bereits zu einem frühen Zeitpunkt drohende Fehlentwicklungen zu erkennen, idealerweise noch bevor sich überhaupt nennenswerte Defizite im Sinne einer Rechenschwäche oder einer umschriebenen Rechenstörung manifestieren können. Für diesen Zweck wurden inzwischen standardisierte Testverfahren vorgelegt, deren prognostische Validität im Rahmen mehrjähriger Längsschnittstudien empirisch abgesichert werden konnte. Damit bestehen nicht nur für das Kindergartenalter gute Möglichkeiten der Früherkennung (Krajewski, in Druck), sondern es liegt auch ein entsprechendes gruppentaugliches Verfahren für die Zeit ab Schuleintritt vor, so dass eine valide Auslese potenziell förderbedürftiger Risikokinder ökonomisch erfolgen und ohne Probleme in den regulären Anfangsunterricht eingebettet werden kann (Ennemoser et al., in Druck).
(3) Möglichkeiten für eine wirksame Prävention
Insbesondere zeigt die vorliegende Studie, wie die Bildungspraxis einem frühzeitig identifizierten Entwicklungsrisiko wirksam entgegentreten kann. Eine entwicklungsorientierte Vorgehensweise, die in dieser Untersuchung mit dem Programm „Mengen, zählen, Zahlen“ (Krajewski et al., 2007) umgesetzt wurde, erscheint unter präventiven Gesichtspunkten vielversprechend. Obwohl im Rahmen der Förderung keinerlei klassische Rechenaufgaben geübt wurden, erzielten auf diese Weise geförderte Kinder im Anschluss größere Zugewinne in ihren Rechenfertigkeiten als alternativ geförderte Kinder. Dies deutet darauf hin, dass eine im vorliegenden Sinne entwicklungsorientierte Förderung einer rein performanzorientierten (also überwiegend auf die Produktion korrekter Lösungen abzielenden) Förderung vorzuziehen ist. Das schließt selbstverständlich nicht aus, dass zu einem späteren Zeitpunkt – sobald ein konzeptuelles Verständnis für Zahl-Größen-Verknüpfungen sicher vorhanden ist – auch ein hinreichender Übungsumfang an „richtigen“ Rechenaufgaben erforderlich ist, um die erworbenen Kompetenzen zunehmend automatisiert anwenden zu können.
Forschungsmethodik
Leider gibt es nach wie vor viel zu wenige Interventionsstudien zur Wirksamkeit präventiver Fördermaßnahmen im schulischen Kontext. Dies gilt nicht nur ganz allgemein für Maßnahmen zur Lernförderung, sondern in besonderem Umfang auch für Maßnahmen, die den Aufbau mathematischer Kompetenzen unterstützen sollen. Erschwerend kommt hinzu, dass es in vielen der verfügbaren Studien nicht umfänglich gelungen ist, grundlegende methodische Standards der pädagogisch-psychologischen Trainingsforschung umzusetzen, so dass die Befunde oft nur eingeschränkt interpretierbar sind. Im Folgenden soll kurz skizziert werden, auf welche Weise in der vorliegenden Studie versucht wurde entsprechende Anforderungen zu berücksichtigen.
Methodischen Standards übergeordnet ist zunächst eine solide theoretische Fundierung. Im vorliegenden Falle bestand diese in einem aktuellen Modell zur Entwicklung mathematischer Basiskompetenzen, aus dem sich sehr präzise ableiten lässt, an welchen Meilensteinen der Entwicklung eine wirksame Präventionsmaßnahme idealerweise ansetzen sollte.
Als Kontrollbedingung diente das in den einbezogenen Schulen übliche Förderangebot, was die Wahrscheinlichkeit verringert, dass die gefundenen Fördereffekte allein aufgrund vermehrter Zuwendung zustande kommen. Da die Förderung – anders als in der Kontrollbedingung – durch externe Fachkräfte durchgeführt wurde, können Zuwendungseffekte zwar nicht ganz ausgeschlossen werden. In dieser (frühen) Phase der Programmevaluation erschien es allerdings noch vorrangig sicherzustellen, dass das Training auch wirklich exakt so umgesetzt wird wie vorgesehen (Sicherstellung der Treatment-Validität; vgl. Patry, 1989), bevor in weiteren Schritten untersucht werden kann, ob dieselben Effekte auch unter weniger gut kontrollierten alltagspraktischen Bedingungen (z. B. bei Durchführung durch reguläre Lehrkräfte) erzielt werden können.
Ein weiterer wichtiger, häufig nicht erfüllter Standard ist die Überprüfung langfristiger Effekte. Um untersuchen zu können, ob kurzfristige Fördererfolge auch längerfristig Bestand haben, wurde drei Monate nach Abschluss der Förderung eine Follow-up-Erhebung durchgeführt. Für die fundierte Bewertung einer Fördermaßnahme ist es zudem von zentraler Bedeutung, dass nicht nur spezifische Effekte auf die trainierten Inhalte untersucht werden. Vielmehr ist darüber hinaus zu überprüfen, in welchem Umfang die Förderung auch tatsächlich Transfereffekte auf nicht explizit geförderte, aber intendierte Inhalte bzw. Kompetenzen nach sich zieht. In der vorliegenden Studie konnte auf diese Weise sichergestellt werden, dass durch das Training mathematischer Basiskompetenzen nicht nur eine bessere Performanz in Aufgaben zur Erfassung dieser Basiskompetenzen erzielt wurde, sondern dass die aufgebauten Kompetenzen langfristig auch wirklich zur effizienteren Lösung von Rechenaufgaben befähigten. Da klassische Rechenaufgaben überhaupt nicht Gegenstand des Trainings waren, konnte durch die Analyse von Transfereffekten zugleich die theoretische Annahme geprüft werden, dass mathematische Basiskompetenzen tatsächlich eine Voraussetzung für den Erwerb elaborierter Rechenfertigkeiten darstellen. Das heißt, die Befunde ermöglichten neben der Wirksamkeitsanalyse auch noch Rückschlüsse auf die Validität der eingangs formulierten Theorien, inklusive der theoretisch angenommenen Wirkmechanismen (Mediatoranalyse).
Manuskript eingereicht: 25.03.2014
Manuskript nach Revision angenommen: 03.09.2014
1 In Vorklassen werden Kinder unterrichtet, die aufgrund verschiedener Defizite zunächst von der Einschulung in eine Regelklasse zurückgestellt wurden und gezielt auf die Anforderungen im Anfangsunterricht vorbereitet werden sollen.
Literatur
(2004). Developmental dynamics of mathematical performance from preschool to grade 2. Journal of Educational Psychology , 96, 699 – 713.
(1997). Grundintelligenztest Skala 1 (CFT 1) (5. Auflage) . Braunschweig: Westermann.
(1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum Associates, Inc.
(1992). Varieties of numerical abilities. Cognition , 44, 1 – 42.
(2010). Training mathematischer Basiskompetenzen als unterrichtsintegrierte Maßnahme in Vorklassen. Empirische Pädagogik , 24, 336 – 352.
(2007). Effekte der Förderung des Teil-Ganzes-Verständnisses bei Erstklässlern mit schwachen Mathematikleistungen. Vierteljahreszeitschrift für Heilpädagogik und ihre Nachbargebiete , 76, 228 – 240.
(2011). Entwicklung und Bedeutung von Mengen-Zahlen-Kompetenzen und eines basalen Konventions- und Regelwissens in den Klassen 5 bis 9. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie , 43, 228 – 242.
(2013). Entwicklungsorientierte Diagnostik mathematischer Basiskompetenzen in den Klassen 5 – 9. In M. Hasselhorn, A. Heinze, W. Schneider & U. Trautwein (Hrsg.), Diagnostik mathematischer Kompetenzen. Tests & Trends N.F. 11 (S. 225 – 240). Göttingen: Hogrefe.
(in Druck). Test zur Erfassung mathematischer Basiskompetenzen ab Schuleintritt (MBK 1+) . Göttingen: Hogrefe.
(2013). Fostering quantity-number competencies in kindergarten and 1st grade: Effects from peer-assisted and teacher-guided training. Poster presented at the International Society for Research in Child Development Biennial Meeting on 20th April in Seattle , Washington, USA.
(2011). Sensori-motor spatial training of number magnitude representation. Psychonomic Bulletin & Review , 18, 177 – 183.
(1988). Children's counting and concepts of number . New York: Springer.
(2004). Defizite numerischer Basiskompetenzen bei rechenschwachen Kindern der 3. und 4. Klassenstufe. Zeitschrift für Pädagogische Psychologie , 18, 31 – 42.
(2000). Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability. Journal of Experimental Child Psychology , 77, 236 – 263.
(2005). Early Identification and Interventions for Students with Mathematics Difficulties. Journal of Learning Disabilities , 38, 293 – 304.
(1995). Teaching for understanding: The importance of central conceptual structures in the elementary school mathematics curriculum. In A. Strauss (Ed.), Educational environments . Norwood, N.J.: Ablex.
(2013). Fostering early numerical skills at school start in children at risk for mathematical achievement problems: A small sample size training study. International Education Studies , 6, 213 – 220.
(2012). Effektive Förderung rechenschwacher Kinder: Eine Metaanalyse. Kindheit und Entwicklung , 21, 1 – 12.
(2010). The importance of number sense to mathematics achievement in first and third grades. Learning and Individual Differences , 20, 82 – 88.
(2003). Vorhersage von Rechenschwäche in der Grundschule . Hamburg: Kovač.
(2005). Vorschulische Mengenbewusstheit von Zahlen und ihre Bedeutung für die Früherkennung von Rechenschwäche. In: M. Hasselhorn, W. Schneider & H. Marx (Hrsg.), Diagnostik von Mathematikleistungen. Test & Trends, N.F. 4 (S. 49 – 70). Göttingen: Hogrefe.
(2007). Entwicklung und Förderung der vorschulischen Mengen-Zahlen-Kompetenz und ihre Bedeutung für die mathematischen Schulleistungen. In: G. Schulte-Körne (Hrsg.), Legasthenie und Dyskalkulie: Aktuelle Entwicklungen in Wissenschaft, Schule und Gesellschaft (S. 325 – 332). Bochum: Winkler.
(2013). Wie bekommen die Zahlen einen Sinn: ein entwicklungspsychologisches Modell der zunehmenden Verknüpfung von Zahlen und Größen. In: M. von Aster & J. H. Lorenz (Hrsg.), Rechenstörungen bei Kindern: Neurowissenschaft, Psychologie, Pädagogik , 2. überarb. Auflage (S. 155 – 179). Göttingen: Vandenhoek & Ruprecht.
(in Druck). Test mathematischer Basiskompetenzen im Kindergartenalter (MBK-0) . Göttingen: Hogrefe.
(2013). Entwicklung und Diagnostik der Zahl-Größen-Verknüpfung zwischen 3 und 8 Jahren. In M. Hasselhorn, A. Heinze, W. Schneider & U. Trautwein (Hrsg.), Diagnostik mathematischer Kompetenzen. Tests & Trends N.F. 11 (S. 41 – 65). Göttingen: Hogrefe .
(2002). Deutscher Mathematiktest für erste Klassen (DEMAT 1+) . Göttingen: Belz Test.
(2007). Mengen, zählen, Zahlen: Die Welt der Mathematik verstehen (MZZ) . Berlin: Cornelsen.
(2008). Kurz- und langfristige Effekte mathematischer Frühförderung im Kindergarten durch das Programm „Mengen, zählen, Zahlen“. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie , 40, 135 – 146.
(2009a). Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a 3-year-longitudinal study. Journal of Experimental Child Psychology , 103, 516 – 531.
(2009b). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year longitudinal study. Learning and Instruction , 19, 513 – 526.
et al. (2011). Mental number line training in children with developmental dyscalculia. Neuroimage , 57, 782 – 95.
(2012). Training Quantity-Number Competencies in Students with Intellectual Disabilities. Journal of Cognitive Education and Psychology , 11, 128 – 142.
(2004). Developmental Dyscalculia and Basic Numerical Capacities: A Study of 8 – 9 Year Old Students. Cognition , 93, 99 – 125.
(2013). Walk the number line – An embodied training of numerical concepts. Trends in Neuroscience and Education , 2, 74 – 84.
(2008). Using Kindergarten Number Sense to Predict Calculation Fluency in Second Grade. Journal of Learning Disabilities , 41, 451 – 459.
(2011). Early place-value understanding as a precursor for later arithmetic performance – A longitudinal study on numerical development. Research in Developmental Disabilities , 32, 1837 – 1851.
(2007). Rechenschwäche/Dyskalkulie. Theoretische Klärungen und empirische Studien an betroffenen Schülerinnen und Schülern . Bern: Haupt.
(2007). The precursors of mathematics learning: working memory, phonological ability and numerical competence. Cognitive Development , 22, 165 – 184.
(1989). Evaluationsstudien zu Forschungszwecken: Ein Beispiel von „kritischem Multiplizismus“. Unterrichtswissenschaft , 17, 359 – 374.
(2008). Playing linear numerical board games promotes low-income children's numerical development. Developmental Science, Special Issue on Mathematical Cognition , 11, 655 – 661.
(2010). Förderung mathematischer Basiskompetenzen in der Grundstufe der Schule für Lernhilfe. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie , 42, 241 – 251.
(1997). Early Training: who, what, when, why, and how? In M. Beishuizen, K. P. E. Gravemeijer & E. C. D. M. van Lieshout (Eds.), The role of contexts and models of mathematical strategies and procedures (S. 239 – 253). Culemborg: Technipress.
(2000). Improving early numeracy of young children with special educational needs. Remedial and Special Education , 21, 27 – 40.
(1998). Stimulation of early mathematical competence. In M. Beishuizen, K. P. E. Gravemeijer & E. C. D. M. van Lieshout (Eds.), The role of contexts and models in the development of mathematical strategies and procedures (pp. 215 – 237). Utrecht: CD-B Press.
(2014). Effekte einer kombinierten Förderung mathematischer Basiskompetenzen und selbstregulierten Lernens bei Risikokindern im Anfangsunterricht. Zeitschrift für Grundschulforschung , 7, 76 – 90.
(2007). Rechenstörungen bei Kindern: Vorläufer, Prävalenz und psychische Symptome. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie , 39, 85 – 96.
(2007). Number development and developmental dyscalculia. Developmental Medicine & Child Neurology , 49, 868 – 873.
(1978). Mind in society: the development of higher psychological processes . Cambridge, MA: Harvard University Press.
(2008). Number games, magnitude representation, and basic number skills in preschooler. Developmental Psychology , 44, 588 – 596.