Why Psychological Assessment Needs to Start Worrying About Model Fit

Anything Wrong With Model Fit?

Imagine, you just received the cleaned and ready-to-go data set of a scale development project that is dear to your heart. Excitedly, you run a confirmatory factor analysis (CFA), for the newly developed scale to see whether it follows the hypothesized factorial structure, say, a unidimensional structure. Good news right away: the fit for the factorial structure is RMSEA = .02, CFI = .98, and SRMR = .03. You conclude, probably just as 99% of other researchers working in assessment would, that you found support for the unidimensional structure.

Maybe – maybe not! Why not, you wonder?

Short and straightforward answer: Because goodness of fit (GoF) in structural equation modeling (SEM) as indicated by fit indices depends on a number of factors and many of these factors (called nuisance parameters) are totally unrelated (!) to the actual degree of model misspecification. Examples of these nuisance parameters are sample size, size of factor loadings of the items, the number of items per latent variable, and so forth (cf. Breivik & Olsson, 2001; Chen, Curran, Bollen, Kirby, & Paxton, 2008; Fan & Sivo, 2007; Garrido, Abad, & Ponsoda, 2016; Heene, Hilbert, Draxler, Ziegler, & Bühner, 2011; Heene, Hilbert, Freudenthaler, & Bühner, 2012; McNeish, An, & Hancock, 2017; Saris, Satorra, & van der Veld, 2009; Yuan, 2005). Put differently, according to Saris, Satorra, and van der Veld cutoff-values for fit indices vary dramatically with the values of nuisance parameters that do not have any connection to the actual level of misspecification. Even worse and contrary to standard practice, there are no “golden rules” that are applicable across data and model constellations, not even for widely used fit indices such as RMSEA, CFI, or SRMR.

Wait a second, you may say. Isn’t there some seminal and highly cited work out there that has established standard cutoff-values? Hu and Bentler (1999) for instance. Yes and no. Yes, seminal and highly cited this work is (exceeding 42,000 according to Google Scholar in August 2017), but applicable as standard for various model types, ranging from unidimensional CFAs to complex SEMs involving many latent variables with a hypothesized complex causal interplay? No!

Although Hu and Bentler (1999) explicitly warned against an overgeneralization of their inferences because they were restricted to only those confirmatory factor analytic models Hu and Bentler specifically investigated, their suggested cutoff-values were rather mindlessly applied to all sorts of SEMs. Jackson, Gillaspy, and Purc-Stephenson (2009) pointed to the fact that almost 60% of studies explicitly used the suggested cutoff-values by Hu and Bentler but the authors “…did not find evidence that warnings about strict adherence to Hu and Bentler’s suggestions were being heeded” (p. 18). This is, in fact, troublesome as the general conclusion from many simulation studies is that the sensitivity of the suggested cutoff-values to detect model misspecifications is disappointingly low for models that are more complex than those used in Hu and Bentler’s simulation study.

The upshot of these simulation studies is that the strong reliance on the cutoff-values by Hu and Bentler (1999) results in a high failure to reject false and often grossly misspecified models. This, in turn, raises questions about the claimed validity of published SEMs and the theories they are based on. Just the other way around, the rate of wrong rejections of correctly specified models can also be severely inflated by these cutoff-values. Nevertheless, failure to reject errors is more serious in model testing as they would erroneously support a theoretical model, whereas a wrong rejection error would result in not supporting a theory, but at the end of the day relying on the established cutoff-values will lead to both: too conservative and too liberal decisions.

Unfortunately, this highly relevant topic has escaped many researchers interested in assessment and has yet to penetrate actual practice. The aims of this editorial are (1) to give some insights into the methodology (i.e., simulation studies) that is used to create knowledge on the behavior of GoF indices; (2) to provide a brief overview of what the gist of this research is; (3) to look ahead and discuss what authors can do about this when writing up their findings. We will not, however, discuss the statistical rationales of the various GoF indices since this is beyond the scope of this editorial. Interested readers should consult, for example, Mulaik (2009) for a detailed account.

The Principle Behind Simulation Studies on Model Fit

Let us first give a conceptual explanation of what a simulation study on model fit assessment actually does to gain a basic understanding of the matter and to illustrate what we know from such studies.

For instance, to investigate the performance of the commonly applied GoF statistic RMSEA, CFI, and SRMR and their suggested cutoff-values of RMSEA < .06, CFI > .95, and SRMR < .08 in a simulation study, we first define a true population model by specifying the number of latent and observed variables and all model parameter values (e.g., variances of exogenous latent variables and observed, latent variable correlations, mean structure, values of factor loadings, etc.). We then construct a misspecified model by setting certain parameters such as loadings or path values to a value other than the actual population value. For instance, we could set cross loadings of some of the items to zero although they might be nonzero in the population, or, we could set a path coefficient between two latent variables to zero in the hypothesized model although it is nonzero in the population model. Alternatively, we could also specify an entirely different model structure by hypothesizing, for instance, a unidimensional latent variable in the misspecified model instead of the multidimensional structure as defined in the population model.

In any of the aforementioned cases of model misspecifications, we would then investigate whether the GoF, given a prespecified cutoff-value, would flag the misspecified model indeed as misfitting. This is done by following these steps: Sample data for a defined sample size (e.g., N = 200 as in the example below) are generated from the population model many times (usually ≥ 1,000) under a distributional model (e.g., multivariate normality). These sample data sets are then analyzed using the misspecified model and the GoFs are calculated for each sample. In the final step, the fraction of GoFs that yielded values worse than their suggested cutoff-values is calculated to determine the correct rejection rate.

The following example further illustrates the idea. Figure 1 depicts two true population models (twodimensional models) and a misspecified model (assuming unidimensionality of the items). Note that in population model A the factor correlation was set to .50, whereas model B shows one of .60. Thus, the degree of misspecification brought about by the unidimensional model is higher under data generated under model A than under model B. Nevertheless, it should still be obvious that two factors sharing 36% of the variance in the q = .60 condition can hardly be regarded as identical factors and that we are confronted with a grossly misspecified model even under this condition. Please note that the factor loadings we chose in the example are quite realistic, for instance when compared to those of the NEO Five-Factor Inventory (NEO-FFI; McCrae & Costa, 2004).

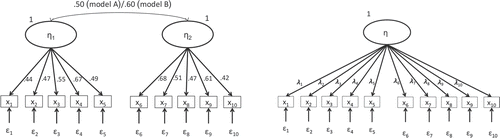
One thousand random sample data replications from multivariate normally distributed observed variables were generated from the true population model under each condition with N = 200 as the typical sample size in the social sciences according to Kline (2015) and Shah and Goldstein (2006). The R package simsem (Pornprasertmanit, Miller, & Schoemann, 2015) was used to carry out the simulation. Model parameters of the misspecified model were then estimated for each of these sample data using maximum likelihood estimation and correct rejection rates and descriptive statistics were then calculated for the suggested cutoff-values (Hu & Bentler, 1999) of the above-mentioned fit indices (the simulation codes can be downloaded from https://osf.io/sm9ha). For the sake of completeness, the power rates of the χ² model test for a significance level of 5% are also reported. The results of the simulation are shown in Table 1.

Table 1 Correct rejection rates for misspecified models. Means and standard deviation of the respective index (in brackets)

Population factor correlations	χ2	RMSEA	CFI	SRMR
ρ = .50	.82 (64.78; 14.60)	.60 (.063; .02)	.95 (.82; .08)	.09 (.07; .01)
ρ = .60	.63 (56.03; 12.77)	.36 (.052; .02)	.84 (.88; .07)	.01 (.06; .01)

Table 1 Correct rejection rates for misspecified models. Means and standard deviation of the respective index (in brackets)

View as image HTML

Although the models are severely misspecified under both conditions, the correct rejection rates of the GoF are disappointingly low, in particular those of the RMSEA and SRMR. Please note how close the mean values of these GoF indices are to their suggested cutoff-values for wellfitting models. Referring to our example given in the section “Anything Wrong With Model Fit?”, applied researchers would then too often claim that the items of the newly developed scale were unidimensional although the true structure is clearly two-dimensional. The point of this small and exemplary simulation was to illustrate that the suggested cutoff-values by Hu and Bentler (1999) cannot be generalized to all sorts of different SEMs and hypothesized latent structures.

What Simulation Studies on Model Fit Know That We Don’t Know

Let us step back and briefly summarize what we know from published simulation studies concerning the performance of the GoF and their suggested cutoff-values to detect misspecifications:

• •
  Sensitivity to detect misspecifications depends on the size of the covariance matrix: More items per factor tend to decrease the RMSEA regardless of the type of misspecification, whereas the CFI tends to worsen, although not always (Breivik & Olsson, 2001; Kenny & McCoach, 2003);
• •
  Sensitivity to detect misspecifications depends on factor loading size: Small factor loadings (i.e., loadings near .40) decrease correct rejection rates and the power of the χ² model test (Hancock & Mueller, 2011; Heene et al., 2011; McNeish et al., 2017). Thus, poorer measurement quality results in seemingly well-fitting models;
• •
  Sensitivity to detect misspecifications partly depends on the type of misspecification (e.g., Chen et al., 2008);
• •
  Sensitivity to detect misspecifications depends on model types (Fan & Sivo, 2007);
• •
  Violations of multivariate normality affect the sensitivity of the fit indices and the χ² model test to detect misspecifications (e.g., Hu & Bentler, 1999).

The bottom line of these findings is: there are no golden rules for cutoff-values, there are only misleading ones. Moreover, inmost of the simulation studies thatwent beyond the models Hu and Bentler (1999) used in their study, their suggested cutoff-values show a poor performance to detect misspecifications raising also questions about the validity of published SEMs having used these cutoff-values.

The Disconnect Between Methodological Research and Standard Practice

The crucial question for EJPA (and other journals) is where the cause of this apparent mismatch between methodological knowledge and actual practice lies and how it can be resolved. McNeish et al. (2017) argue that the high level of technical detail involved in simulation studies inhibits their widespread perception and Marsh, Hau, and Wen (2004) highlight that the lack of clear and applicable guidelines (“no golden fleece”) makes it difficult for researchers who use SEM as an everyday tool for investigating contentrelated questions to integrate these findings into their practice.

To some extent, GoF indices and their cutoff-values will remain ambiguous. It is an undisputable fact that they are (heavily) influenced by circumstantial variables unrelated to model fit. Nobody – and this editorial for the very least – can make the world of GoF easier as it is, and yet, there are some guidelines that at least can bring some light into the dark. This editorial is driven in the spirit and the hope that it helps researchers to find a more adequate way of reporting and evaluating model fit and in particular so when they submit their article to the European Journal of Psychological Assessment.

The World of Model Fit Just Ain’t Simple – and Some Practical Recommendations

Some have suggested that, as an alternative, the χ² should only be used. However, the χ² test suffers from similar problems: Its power to detect misspecifications depends on sample size and size of the factor loadings (e.g., Hancock & Mueller, 2011; Heene et al., 2011; McNeish et al., 2017). It is nevertheless in general more statistically powerful than the suggested cutoff-values as many of the cited simulation studies have shown.

Its use, however, is often discouraged in applied papers using a false logic: it is true that with large sample sizes, even small discrepancies between the model-implied and observed covariance matrix will result in a significant test statistic, yet the reverse does not necessarily hold: a significant χ² test based on a large sample does not imply small discrepancies but could point to large discrepancies. We therefore agree with Ropovik (2015) that, in case of a significant χ² test, “…it should not be concluded the model approximates the data and ascribe the model test failure to statistical power without a careful inspection of local fit.”

What is therefore needed besides the assessment of global model fit is an inspection of local misspecifications (e.g., missing paths, correlations), regardless of how impressive the GoF indices of a particular study might be. Saris et al. (2009) developed a misspecification detection method based on the expected parameter change in combination with the modification index (MI) and the a priori power of the MI test. Oberski (2010) provides free software to run a misspecification search, which is also implemented in the R package “semTools” (Contributors, 2016). In addition to this, Ropovik (2015) provides a detailed nontechnical overview of various misspecification methods.

Admittedly, the suggested methods mostly apply to misspecifications concerning missing paths, factor correlations, error correlations, or cross loadings.

We furthermore encourage authors to proactively tackle the issue of model fit by running analyses on local misspecification or by critically discussing cutoff-values of GoF and by making reference to published simulation studies.