Entwicklungs- und spielbasierte Förderung früher arithmetischer Konzepte
Abstract
Zusammenfassung.Hintergrund: Die Subjektwissenschaftliche Lerntheorie betrachtet Lernprozesse vom Standpunkt des Subjektes. Dabei wird ein besonderer Fokus auf Begründungsstrukturen für gelingende oder nicht gelingende Lernhandlungen gelegt. Die subjektwissenschaftliche Perspektive scheint gerade für die Betrachtung von Lernprozessen in der Alphabetisierung und Grundbildung gewinnbringend, da bisherige (negative) Lernerfahrungen, unterschiedlich zusammengesetzte Kompetenzen sowie spezifische Bildungsziele (wie z.B. gesellschaftliche Teilhabe) auf besondere Weise das Lernen beeinflussen können. Grundbildungszentren (GBZen) können als regionale Anlaufstellen für unterschiedliche Fragestellungen bezüglich der Grundbildung und Alphabetisierung Erwachsener Lernenden gelten. Dabei halten GBZen sowohl niedrigschwellige Lernangebote für Menschen mit Alphabetisierungs- und Grundbildungsbedarfen vor, als auch regionale Netzwerk- und Kooperationsstrukturen, um das Umfeld der Lernenden zu sensibilisieren. Methoden: Anhand von zwölf Interviews und vier Selbstberichten, die im Rahmen einer Evaluationsstudie generiert wurden, wurde folgende Fragestellung sekundäranalytisch beantwortet: Welches Potential haben die GBZen Lernprozesse subjektorientiert zu gestalten? Ergebnisse und Diskussion: Die Ergebnisdarstellung erfolgt anhand einer institutionellen, interaktionellen sowie individuellen Ebene. Die Ergebnisse zeigen, dass die Struktur der GBZen eine wesentliche Vorbedingung darstellt, Lernenden subjektorientiert zu unterstützen, sich das Potenzial in vollem Umfang aber nur durch das Zusammenwirken aller drei Ebenen entfalten kann.
Abstract.Background: Subject-scientific learning theory describes learning processes from the point of view of the subject. Thereby, a special focus is put on justification structures for successful or unsuccessful learning actions. The subject-scientific perspective seems to be especially profitable for the consideration of learning processes in literacy and adult basic education, since previous (negative) learning experiences, differently composed competencies as well as specific educational goals (such as social participation) can influence learning in a special way. Adult Basic Education Centers can be considered as regional contact points for different questions concerning basic education and literacy of adult learners. Adult Basic Education Centers provide low-threshold learning opportunities for people with literacy and basic education needs, as well as regional networking and cooperation structures to sensitize the learners' environment. Methods: Based on twelve interviews and four self-reports generated in the course of an evaluation study, the following question was answered in a secondary analytical way: What is the potential of Adult Basic Education Centers to make learning processes subject-oriented? Results and discussion: The results are presented on an institutional, interactional and individual level. The results show that the structure of the Adult Basic Education Centers is an essential precondition to support learners in a subject-oriented way, but that the potential can only unfold to its full extent through the interaction of all three levels.
Einleitung
Unter Forschenden zum Erwerb arithmetischen Wissens herrscht weitgehende Einigkeit darüber, dass Kinder bereits im Vorschulalter wesentliches arithmetisches Wissen erwerben (z.B. Hartmann, Ehlert & Fritz, 2019; Slusser, 2019; Wynn, 1992). In den vergangenen Jahren konnten mehrere Studien nachweisen, dass das arithmetische Wissen, das Kinder am Beginn der Grundschulzeit besitzen, von großer prädiktiver Bedeutung für den weiteren Lernverlauf ist (Aunio & Niemivirta, 2010; Krajewski & Schneider, 2009; Kuhn, Schwenk, Souvignier & Holling, 2019; Martin, Cirino, Sharp & Barnes, 2014).
Verschiedene Studien betonen unterschiedliche Prädiktoren. Wesentliche spezifische Prädiktoren sind Zählfertigkeiten (Desoete, Stock, Schepens, Baeyens & Roeyers, 2009; Martin et al., 2014), Größenvergleiche zweier Zahlen (Hawes, Nosworthy, Archibald & Ansari, 2019; Le Corre, 2014), die Verknüpfung von Zahlen und Mengen (Fritz, Ehlert & Leutner, 2018; Krajewski & Schneider, 2009), Teil-Teil-Ganzes-Beziehungen (Langhorst, Ehlert & Fritz, 2012) sowie präzise räumliche Vorstellungen von Zahlpositionen auf dem Zahlenstrahl (Dietrich, Huber, Dackermann, Moeller & Fischer, 2016).
Angesichts der großen Bedeutung frühen arithmetischen Wissens für das Mathematiklernen in der Schule kommt dessen Förderung eine zentrale Rolle bei der Prävention und Intervention von Rechenschwierigkeiten zu. Um geringe Lernausgangslagen nicht zu substantiellen Lernrückständen anwachsen zu lassen, gilt eine frühe Förderung arithmetischen Wissens als wesentliche Maßnahme zur Prävention von Rechenschwierigkeiten (Dowker, 2005). Aktuell gibt es eine Vielzahl von zielgerichteten Trainings, die auch in jungem Alter arithmetisches Wissen effektiv vermitteln können (Chodura, Kuhn & Holling, 2015).
Theorie
Spielbasierte Förderung
Einen vor allem in Bezug auf junge Kinder relevanten Ansatz, frühe mathematische Förderung zu gestalten, stellen spielbasierte Fördermaterialien dar. Hierbei werden die zu fördernden mathematischen Inhalte mit typischen Elementen von Spielen verknüpft. Insbesondere im Kindergartenalltag sind spielbasierte Förderansätze die Regel (Smidt, 2013). Aus didaktischer Sicht hebt Gasteiger (2010) vor allem den konstruktivistischen Aspekt spielbasierter Förderung hervor: Die Lerninhalte werden nicht formal instruiert, sondern die Kinder können sie im Rahmen des Spiels selbst entdecken und erwerben. Das Spiel gestaltet demnach im Wesentlichen den Rahmen, in dem der Lernprozess geschieht.
Spiele haben sich als effektiv für die Vermittlung arithmetischen Wissens erwiesen. Beispielsweise haben Jörns, Schuchardt, Mähler und Grube (2013) zehn Spiele zur frühen mathematischen Förderung im Zahlenraum bis Zehn entwickelt und im Vorschulbereich eingesetzt. Die Spiele folgen einem Modell früher arithmetischer Kompetenzen und erfordern das Benennen arabischer Zahlen, das Zählen kleiner Mengen, das Aufsagen der Zahlwortreihe vorwärts und rückwärts sowie das Addieren kleiner, nicht-sichtbarer Mengen. Dabei konnten insgesamt zwar signifikante Lerneffekte festgestellt werden, diese galten jedoch nicht für alle Bereiche frühen arithmetischen Wissens in gleicher Weise. So verbesserten sich die Zähl- und Rechenfertigkeiten der Experimentalgruppe signifikant stärker als die der Kontrollgruppe. Bezüglich des Benennens arabischer Zahlen sowie dem Mengenvergleich konnten keine Unterschiede zwischen den Gruppen berichtet werden (Jörns et al., 2013). In einer Folgestudie konnte gezeigt werden, dass die Passung der konzeptuellen Anforderungen der Spiele zu den Lernvoraussetzungen der Kinder deren Lerneffekt wesentlich beeinflussten (Jörns, Schuchardt, Grube Mähler, 2014). Während leistungsschwächere Kinder vor allem von den Lernspielen mit geringeren konzeptuellen Anforderungen profitierten, verzeichneten die leistungsstärkeren Kinder insbesondere bei den Spielen Lerneffekte, die höhere konzeptuelle Anforderungen an sie stellten. Für eine effektive Förderung aller Kinder mit unterschiedlichen Lernvoraussetzungen ist es offenbar nicht ausreichend, Spiele lediglich bereitzustellen, sondern diese sind an die Lernvoraussetzungen der Kinder anzupassen.
Dieser Zusammenhang wird besonders deutlich in Studien, die Effekte linearer Brettspiele auf arithmetisches Wissen untersuchten. Siegler und Ramani (2008) ließen 36 Kinder der ersten Klasse vier Einheiten eines Brettspiels spielen, bei dem die Kinder durch Würfeln eine Spielfigur über zehn gleichgroße Felder von links nach rechts bewegen sollten. Durch Dazuzählen der gewürfelten Zahl bestimmten die Kinder die neue Position ihrer Figur. Im Vergleich zu Kindern einer nicht trainierten Kontrollgruppe verbesserten die Kinder der Experimentalgruppe ihre Leistungen beim Einschätzen von Zahlpositionen auf dem Zahlenstrahl signifikant. Eine zweite Experimentalgruppe, bei der die Zahlen auf dem Spielbrett durch Farben ersetzt wurden, zeigte keine Verbesserung (Siegler & Ramani, 2008).
Die Ergebnisse dieser Studien legen nahe, dass Rechenförderungen, die auf Brettspielen basieren, vor allem die Leistungen verbessern, die auf zählenden Strategien basieren. So fördern lineare Brettspiele vor allem eine ordinale Vorstellung von Zahlen und verbessern dementsprechend insbesondere die Orientierung auf dem Zahlenstrahl oder zählbasierte Rechenaufgaben.
Der unmittelbare Zusammenhang zwischen Lerneffekt, Spieldesign und Lernvoraussetzungen der Kinder zeigt die Notwendigkeit auf, spielbasierte Mathematikförderung einerseits an die gewünschten Lernziele und andererseits an die Lernvoraussetzungen der Kinder anzupassen. Damit stellt sich die Frage, wie die Passung zwischen arithmetischem Förderinhalt, Lernvoraussetzungen der Kinder und Spieldesign gewährleistet werden kann. Eine theoriegeleitete Strukturierung des Erwerbs arithmetischer Konzepte kann eine geeignete Grundlage sein, um spielbasierte Förderung effektiv zu gestalten.
Entwicklung arithmetischer Konzepte
Der Erwerb arithmetischer Konzepte kann in entwicklungsorientierten Modellen beschrieben werden. Für den deutschsprachigen Raum wurden in den vergangenen Jahren verschiedene Modelle vorgestellt (z.B. Fritz et al., 2018; Krajewski & Schneider, 2009; von Aster & Shalev, 2007). Einige dieser Modelle weisen strukturelle Gemeinsamkeiten auf, unterscheiden sich jedoch in den Details, wie der Erwerb arithmetischer Konzepte hierarchisiert wird (Fischer, Roesch & Moeller, 2017).
Fritz et al. (2018) haben ein Entwicklungsmodell arithmetischer Konzepte vorgelegt, das einerseits eine breite theoretische Grundlage besitzt, andererseits aber auch in Längsschnittstudien empirisch validiert worden ist (Fritz et al., 2018). Das Modell beschreibt insgesamt sechs Levels, die hierarchisch aufeinander aufbauen. Das bedeutet, dass die Konzepte eines früheren Levels notwendig sind, um die Konzepte späterer Levels zu entwickeln. Im Laufe der Entwicklung werden die arithmetischen Konzepte, wie sie das Modell beschreiben, immer weiter elaboriert. Sie wechseln einander also nicht in distinkten Stufen ab, sondern sind wie in einem Modell überlappender Wellen miteinander verwoben (Siegler & Alibali, 2005). Da bisher nur die ersten fünf Levels spielbasiert umgesetzt wurden, werden an dieser Stelle auch nur die ersten fünf Levels dargestellt.
Level I: Zählzahl
Das Modell beginnt mit der Einsicht der Kinder, Zahlworte zum Zählen einsetzen zu können. Zählen lernen ist ein zentraler Bestandteil des vorschulischen arithmetischen Wissens der Kinder (Slusser, 2019; Wynn, 1992). Dabei erwerben Kinder die Zahlwortreihe zunächst ähnlich einem Gedicht als Abfolge von Worten, die nicht mit Anzahlen verknüpft sind (Gelman & Gallistel, 1978). Dieses sogenannte prozedurale Zählen bildet die Grundlage für die Fähigkeit, kleine Anzahlen sicher zu bestimmen (Desoete et al., 2009; Fritz et al., 2018).
Der Erwerb präziser Zählfertigkeiten geschieht schrittweise in einem Prozess des Zuordnens von Zahlworten zu Zählobjekten (Hartmann et al., 2019): Zunächst lernen Kinder, ein Element verlässlich zu zählen; größere Zahlen führen zu zufälligen Antworten. Anschließend lernen Kinder die Bedeutung von „Zwei“ mit genau zwei Objekten zu verknüpfen. Auch zu diesem Zeitpunkt führen größere Zahlen zu zufälligen Antworten. Sukzessiv erwerben Kinder präzise Zählfertigkeiten von drei und vier Objekten. Teile der diesbezüglichen Forschung gehen davon aus, dass mit Erwerb des präzisen Konzepts der „Vier“ auch präzise Konzepte größerer Zahlen erworben werden (Le Corre & Carey, 2007).
Level II (ordinaler Zahlenstrahl):
Zählfertigkeiten präzisieren die Beziehung zwischen Zahlworten und Zählobjekten, geben jedoch keinen Aufschluss über die Beziehungen zwischen den Zahlen selbst. Basierend auf der festen Ordnung der Zahlwortreihe lernen Kinder auf dem zweiten Level, dass auch Zahlen eine Ordnung besitzen: Größere Zahlen kommen später in der Zahlwortreihe, kleinere früher (Le Corre, 2014). Auf der Grundlage dieses „Später-Größer-Prinzips“ können Kinder Zahlen hinsichtlich der Größe vergleichen. Basierend auf der ordinalen Vorstellung von Zahlen und ihrer Ordnung können Kinder Schemata des Vermehrens und Verminderns auf einfache Rechenaufgaben anwenden (Resnick, 1983).
Mit der Entwicklung einer ordinalen Zahlvorstellung geht auch eine räumliche Vorstellung des mentalen Zahlenstrahls einher (Dehaene, 2013; Fritz et al., 2018). Kinder beginnen, Zahlen in Schreibrichtung in aufsteigender Reihenfolge zu repräsentieren. Dabei ist ihre Einschätzung von Positionen auf dem Zahlenstrahl zunächst logarithmisch skaliert; d.h. kleine Zahlen werden zu weit rechts, große Zahlen zu weit links vermutet. Erst im Laufe der Grundschulzeit wird die Repräsentation von Zahlen linear (Thompson & Opfer, 2010).
Level III (Kardinalität):
Auf dem dritten Level gewinnen Zahlen eine kardinale Bedeutung: Die Zahl Fünf steht für eine Menge aus fünf Elementen (Fritz et al., 2018). Ausgehend von einem solchen Verständnis können Kinder einfache Rechenaufgaben durch Weiterzählen lösen („count-on“-Strategie, Fuson 1988). Ein mengenbezogener Zahlbegriff erlaubt auch das flexible Zerlegen von Zahlen in kleinere Zahlen (z.B. 5 in 2 und 3), wodurch Zahlen zu „composite units“ werden (Steffe, 1992). Die Einsicht, Zahlen in kleinere Zahlen zerlegen zu können, macht die Anwendung flexiblerer Rechenstrategien erst möglich (z.B. 8 + 5 = 8 + 2 + 3 = 10 + 3).
Das kardinale Zahlkonzept bildet auch die Grundlage, um strukturierte Mengen größer als Vier quasi-simultan auf einen Blick zu erfassen. Kleine Mengen bis zu vier Elementen können mit einem Blick (simultan) erfasst werden, das sogenannte „Subitizing“. Diese Fähigkeit entwickeln Kinder in der Regel bis zum Schuleintritt (Clements, Sarama & MacDonald, 2019). Um größere Mengen rasch und ohne zu zählen zu erfassen, bedarf es strukturierter Anordnungen, die die Gesamtmenge so in Teilmengen zerlegen, dass diese einzeln simultan erfasst werden können. Starkey & McCandliss (2014) sprechen vom sogenannten „Groupitizing“. Empirische Studien konnten die Fähigkeit zum Groupitizing als Prädiktor von Rechenfertigkeiten ausweisen (Arndt, Sahr, Opfermann, Leutner & Fritz, 2013).
Mit dem Wandel hin zu einer mengenbasierten Zahl_vorstellung ändern sich auch Vorstellungen von Operationen und Zahlbeziehungen. Zum Größenvergleich zweier Zahlen müssen Kinder nun nicht mehr die Zahlwortreihe durchgehen und auf die Positionen der zu vergleichenden Zahlen achten, sondern können dies auf Grundlage der enthaltenen Mengen tun. Addition und Subtraktion sind auf Level III nicht mehr Prozesse des Vor- und Rückwärtszählens, sondern beschreiben das Zusammenfügen oder Zerlegen einer Zahl aus oder in kleinere Zahlen.
Level IV (Teil-Teil-Ganzes-Konzept):
Ausgehend vom Konzept der “composite unit”, das die Zerlegbarkeit von Zahlen in kleinere Zahlen beschreibt, flexibilisieren Kinder auf dem vierten Level ihre Vorstellungen von den Beziehungen zwischen Teilen und Ganzem. Dieses Teil-Teil-Ganze-Konzept wird vielfach als wesentlicher Meilenstein in der kindlichen Entwicklung der Zahlvorstellungen betrachtet (Fuson, 1988; Resnick, 1983). Kinder lernen, dass die Beziehung zwischen Teilen und Ganzem determiniert ist und Zahlen somit feste Teil-Teil-Ganzes-Tripel bilden (z.B. 2, 3 und 5). Dazu verbinden sie ihre nicht-zahlbezogenen Vorstellungen zum Zerlegen und Zusammenfügen mit den kardinalen Vorstellungen zum Zerlegen von Zahlen (Resnick, 1983). Dieses Wissen versetzt Kinder in die Lage, Zahlen flexibel zu zerlegen und die dritte Menge zu bestimmen, wenn zwei Mengen bekannt sind (Huttenlocher, Jordan & Levine, 1994). Damit werden auch Aufgaben zur Ausgangsmenge (? + 3 = 5) und zur Austauschmenge (2 + ? = 5) lösbar.
Level V (Relationalität):
Mit dem fünften Level geht eine weitere Veränderung der Zahlvorstellung einher: Zahlen können nun Abstände zwischen Zahlen repräsentieren (Stern, 1998). Zahlen drücken auf diesem Level daher auch die Relationen zwischen anderen Zahlen aus. Damit beschreibt eine Zahl (z.B. 2) nun eine ganze Klasse von Differenzen zwischen Zahlen (z.B. 4 & 6 oder 7 & 9).
Besondere Bedeutung bekommt das relationale Zahlkonzept auch dadurch, dass es eine wesentliche konzeptuelle Basis für die Vorstellung der Multiplikation als wiederholte Addition bildet (Long, 2015). In der Terminologie von Steffe (1992) wird die Zahl damit zur „iterable unit“. In ähnlicher Weise unterstützt die Relationalität die Entwicklung tragfähiger Stellenwertvorstellungen. Der „Zehner“ als wesentlicher Bestandteil früher Stellenwertvorstellungen wird erst durch seine regelmäßige Wiederholbarkeit zur Bündeleinheit (Cobb & Wheatley, 1988; Herzog, Ehlert & Fritz, 2019).
Entwicklungs-und spielbasierte Förderung
Material
Mit dem „Erdmännchen-Blitzblick-Memo“ (EBM, Herzog & Fritz, 2018) liegt ein spielbasiertes Mathematikfördermaterial vor, das die Prinzipien Entwicklungsorientierung und Spielbasierung vereint. Die Spielvarianten basieren auf dem empirisch validierten Entwicklungsmodell arithmetischer Konzepte von Fritz et al. (2018). Für jedes der ersten fünf Levels des Modells existieren spezifische Spielvariationen, die die jeweiligen relevanten Lerninhalte abdecken (s. Elektronisches Supplement ESM1). Durch die gezielte Anpassung der Spielvariationen an die Anforderungen der jeweiligen Level wird eine hohe Passung zwischen Lerngegenstand und Lernvoraussetzungen erreicht. Da die notwendigen Lerninhalte im Vorfeld durch die Verankerung im Entwicklungsmodell feststehen, ist die Passung kein Zufall, sondern Resultat des Spieldesigns.
Die grundlegende Struktur des EBM ist an ein klassisches Memory-Spiel angelehnt, das viele Kinder im Vor- und Grundschulalter bereits kennen. Wiederkehrendes Spielelement ist das Zuordnen von Karten mit verschiedenen Zahldarstellungen im Zahlenraum bis 20. Zahlen werden im EBM als Ziffern sowie durch Mengen dargestellt. Die Mengen werden durch konkrete Bilder – bspw. Löwen, Affen oder die namensgebenden Erdmännchen – sowie durch abstrakte Figuren (Kreise, Rechtecke, Polygone; s. ESM1) präsentiert. Dabei folgen die Mengendarstellungen zwei wesentlichen Strukturierungsprinzipien: der Darstellung in Zerlegungen in strukturierte Teilmengen bis zu vier Elementen sowie in Reihen zu fünf Elementen gemäß der „Kraft der Fünf“ (s. ESM1). Ziel beider Strukturierungen ist die Erfassung der Gesamtmenge ohne auf Zählprozesse angewiesen zu sein.
Die Zerlegung in Teilmengen von bis zu vier Elementen nutzt die Fähigkeit zum „Groupitizing“ aus. Hierbei ist es nicht nötig, die Elemente auf den Karten zu zählen, weil die Teilmengen kleiner als vier und damit im Bereich des Subitizings liegen. Da diese Strukturierung viel Platz auf den Karten benötigt, kann sie effektiv nur im Zahlenraum bis Zehn genutzt werden. Theoretischer Hintergrund für die Reihenanordnung ist die sogenannte „Kraft der Fünf“ (Gaidoschik, 2007). Durch die regelmäßige Anordnung in Reihen bis zu fünf Elementen können die Anzahlen bestimmt werden, ohne sie zu zählen. Die vollen Reihen können in Fünferschritten addiert werden. Die Anzahlen in den unvollständigen Reihen können mit einem Blick erfasst werden, da maximal vier Elemente enthalten sind, die sich somit innerhalb des Zahlbereichs des Subitizings befinden.
Spielvarianten
Die Spielvarianten für Level I fokussieren den Erwerb präziser Zählfertigkeiten (s. Tab. E1 im ESM1). Dazu werden die Karten offen ausgelegt, die Elemente der Karten können gezählt werden. Zu den Varianten auf Level I gehört auch die Zuordnung von Ziffern und Zahlen. Da Zählfertigkeiten sukzessive erworben werden, sollte der Zahlbereich entsprechend angepasst werden (Slusser, 2019). Dementsprechend kann mit einem kleinen Zahlbereich, in dem das Kind bereits zählen kann (z.B. 3), angefangen werden und dieser nach und nach erweitert werden.
Auf Level II sollen die Kinder eine ordinale Vorstellung von Zahlen entwickeln. Aus diesem Grund sind auf diesem Level vor allem Spielvarianten mit linearen Anordnungen zu finden (s. Tab. E2 im ESM1). Dazu können die Ziffernkarten in aufsteigender Folge sortiert oder falsche Reihen korrigiert werden. Eine Möglichkeit, die Ziffernreihe zu sortieren ist, eine ungeordnete Reihe verdeckt hinzulegen. Das Kind darf jeweils zwei Karten aufdecken. Sind diese beiden Zahlen in der richtigen Reihenfolge, werden sie wieder verdeckt; andernfalls dürfen sie getauscht werden. Auf diese Weise wird die Ziffernreihe der Größe nach sortiert. Zu den Konzepten auf diesem Level gehört auch der Größenvergleich zweier Zahlen auf Basis der Zahlwortreihe. Eine entsprechende Spielvariante ist, den Kindern je einen Stapel Ziffernkarten zu geben. Die Spieler decken alle gleichzeitig die oberste Karte auf. Wer als erstes erkennt, welche Zahl die größte (oder kleinste) ist, darf die Karten behalten. Auf diesem Level darf die Zahlwortreihe als Hilfsmittel oder zur Absicherung aufgesagt werden.
Wesentliches Element der Spielvarianten auf Level III ist die Zuordnung von Ziffern und Mengen (s. Tab. E3 im ESM1). Dazu können klassische Memoryvarianten mit Ziffern und Mengenkarten gespielt werden, die einander zuzuordnen sind. Da Level III die konzeptuelle Grundlage für das Groupitizing darstellt, sollten die Kinder in diesen Varianten nach und nach daran gewöhnt werden, die Anzahl der Elemente auf einer Karte nicht mehr zählend, sondern (quasi-)simultan zu erfassen. In einer weiteren Spielvariante kann das Kind die Mengenkarten der Größe nach sortieren. Dazu muss das Kind nun nicht mehr die Position innerhalb der Zahlwortreihe bestimmen, sondern kann die Karten basierend auf der Mächtigkeit der entsprechenden Menge vergleichen. Als Hilfsmittel kann anfänglich eine geordnete Ziffernreihe hinzugezogen werden. Um die Verknüpfung von Mengen und Zahlen mit den Operationen Addition und Subtraktion zu verbinden, können einfache Rechenaufgaben mit den Mengenkarten nachgestellt werden.
Die Spielvarianten auf Level IV nehmen vor allem das Teil-Teil-Ganze-Konzept in den Blick (s. Tab. E4 im ESM1). Dazu werden die Karten auf einem T-förmigen Feld angeordnet: Im großen oberen Feld wird die Gesamtmenge platziert, während unten die Teilmengen gelegt werden. Auch hier können Ziffern- und Mengenkarten gemischt werden. In einer Variante des klassischen Memorys wird ein Teil-Teil-Ganzes-Tripel geformt: Eine Karte wird gezogen, die das Ganze darstellt und die Aufgabe beim Aufdecken der Karten ist es, zwei Karten zu finden, die sich als zwei Teile zum Ganzen aufsummieren lassen. Auch diese Variante kann mit Addition und Subtraktion verknüpft werden, indem sie als Illustration von Lückenaufgaben (s.u.) dient. Ebenso können diese Varianten mit typischen Formaten aus dem Unterricht wie dem Zahlenhaus oder der Zahlenmauer kombiniert werden. Fortgeschrittene Kinder können auch mehr als zwei Teilmengen bilden.
Im Zentrum der Spielvarianten für Level V stehen die Gleichabständigkeit der Zahlen auf dem Zahlenstrahl sowie das Verständnis von Zahlen als Repräsentanten von Abständen zwischen Zahlen (s. Tab. E5 im ESM1). Zu diesem Zweck werden die auf vorherigen Levels bereits genutzten Verknüpfungen von Additions- und Subtraktionsaufgaben mit dem Zahlenstrahl als Veranschaulichungsmittel kombiniert. Auf diese Weise werden Aufgaben zum Teil-Teil-Ganzes-Konzept (z.B. 14 – ? = 3) in das Konzept der Relationalität eingebettet. So verstanden fragt die Rechenaufgabe nicht mehr nach dem fehlenden zweiten Teil, sondern nach der Differenz (bzw. dem Abstand auf dem Zahlenstrahl).
Die Anlehnung an ein theoretisch begründetes und empirisch belegtes Entwicklungsmodell erlaubt das gezielte Elaborieren bestehender Konzepte und die Vermittlung neuer Konzepte. Ein wesentliches Prinzip der Förderung mit dem EBM ist der Einsatz ähnlicher Formate auf unterschiedlichen Levels. Dazu werden Spielvarianten in der Durchführung nur geringfügig verändert, hinsichtlich des zu vermittelnden Konzeptes jedoch spezifisch angepasst. Dies wird deutlich am Beispiel des klassischen Memorys. Die grundlegende Spielidee ist in allen Varianten sehr ähnlich: Die Karten werden verdeckt auf dem Tisch ausgelegt und paarweise von einem Spieler aufgedeckt. Passen die Karten zusammen, darf der Spieler sie behalten, andernfalls ist der nächste Spieler an der Reihe. In den Varianten auf Level I und Level III passen Karten immer dann, wenn sie die gleiche Anzahl zeigen. Auf Level I ermitteln Kinder dies zählend oder durch Subitizing und auf Level III mittels Groupitizing. Auf Level IV wird eine Karte gezogen, die das Ganze bildet und es werden zwei Karten aufgedeckt, die dann passen, wenn sie mit der Zielzahl ein Teil-Teil-Ganzes-Tripel ergeben. Die Adaptionen der Memory-Varianten an die konzeptuellen Anforderungen des Modells veranschaulichen auch die Verschränkungen zwischen den Levels des Modells (Fritz et al., 2018).
Forschungsfragen
In dieser Studie soll geprüft werden, in welchem Maße die frühen mathematischen Konzepte von Kindern im Vor- und Grundschulalter mit einem spielbasierten Fördermaterial, das an ein Entwicklungsmodell angelehnt ist, gefördert werden können. Dieses Vorhaben wird mithilfe mehrerer Forschungsfragen verfolgt.
- 1.Kann das konzeptuelle arithmetische Wissen von Vor- und Grundschulkindern durch spielerische und an ihre Lernvoraussetzungen angepasste Förderung mit dem EBM gesteigert werden?
- 2.Unterscheiden sich die Lernzuwächse der geförderten Kinder signifikant von der Entwicklung von Kindern ohne Training?
- 3.In welchem Maße unterscheiden sich die Trainingseffekte in Abhängigkeit vom arithmetischen Vorwissen der Kinder?
- 4.Auf welche Weise beeinflussen domänen-unspezifische Faktoren wie sprachliche oder kognitive Fähigkeiten die Lernzuwächse beim Spielen mit dem EBM?
Methode
Design und Stichprobe
Die Studie folgte einem Prä-Post-Follow-up-Design mit je einer Experimentalgruppe (EG) und einer passiven Kontrollgruppe (KG) für die Altersbereiche Kindergarten (N = 67, 34 Mädchen, MAlter = 65.77 Monate) und erste Klasse (N = 60, 27 Mädchen, MAlter = 82.33 Monate). Die Kindergartenkinder wurden ein halbes Jahr vor der Einschulung gefördert, die Grundschülerinnen und Grundschüler ein halbes Jahr nach der Einschulung. Der Prätest wurde unmittelbar vor Beginn der Förderung durchgeführt, der Posttest direkt nach dem Ende der Förderung. Etwa drei Monate nach dem Posttest erfolgte ein Follow-up-Test, um längerfristige Effekte der Förderung zu untersuchen.
Beide Stichproben wurden zufällig in eine Experimental- und in eine passive Kontrollgruppe eingeteilt. Die Kinder der beiden Experimentalgruppen wurden über einen Zeitraum von sechs bis acht Wochen mit dem EBM gefördert. Die Förderung bestand aus den angeleiteten Spielen mit dem EBM, die adaptiv nach den Lernvoraussetzungen der Kinder ausgewählt wurden. Dabei erhielten die Kinder im Kindergarten zwischen sieben und zwölf (M = 9.79, SD = 1.15) und die Kinder in der ersten Klasse zwischen sieben und zehn (M = 9.60, SD = .81) Fördersitzungen. In der Schule fanden die Fördersitzungen in separaten Räumen (z.B. Förderräume, Bibliothek) während des regulären Mathematikunterrichts statt, sodass die Kinder in den Experimentalgruppen nicht mehr angeleitete Lernzeit mit mathematischen Inhalten hatten als die Kinder der Kontrollgruppen. Die Förderung wurde von geschulten Studierenden in Kleingruppen mit bis zu drei Kindern durchgeführt. Die Fördergruppen wurden mit Blick auf ein vergleichbares mathematisches Vorwissen im Sinne des Modells von Fritz et al. (2018) zusammengestellt. Hierzu wurden Tests der MARKO-Reihe (Mathematik und Rechenkonzepte) eingesetzt. Das arithmetische Vorwissen im Kindergarten wurde mit dem MARKO-S (Ehlert, Fritz & Ricken, 2020) erfasst, sodass hier vier Gruppen (Level I, II, III und III+) gebildet werden konnten. Kinder aus der Gruppe „Level I“ haben das erste Level noch nicht erreicht und erarbeiten dieses gerade; analog wurden die Gruppen „Level II“ und „Level III+“ gebildet. Da der MARKO-S nicht zwischen den Levels IV bis VI des Modells nach Fritz et al. (2018) differenziert, die Gruppe, die das dritte Level bereits erworben hat aber nicht ohne Förderung bleiben sollte, wurde diese Gruppe mit III+ bezeichnet. In der ersten Klasse wurde das arithmetische Wissen mit dem MARKO-D (Ricken, Fritz & Balzer, 2013) erfasst. Hier hatten alle Kinder mindestens das erste Level erreicht. Da das EBM keine Spielvarianten für Kinder auf Level VI bereithält, wurden Kinder, die das fünfte Level erreicht hatten nicht in die Studie mit einbezogen. Analog zum Vorgehen im Kindergarten wurden hier die Gruppen „Level II“ bis „Level V“ gebildet.
Zunächst werden die Lernausgangslagen (arithmetisches Vorwissen, Alter sowie kognitive und sprachliche Fertigkeiten) der EG und KG paarweise verglichen, um die Vergleichbarkeit der Gruppen zu prüfen. Um zu prüfen, ob sich das arithmetische Wissen der Kinder durch den Einsatz des EBM verbessert, wird die Entwicklung der Mathematikleistung über die drei Messzeitpunkte hinweg zwischen den Kindern der EG und der KG nach Altersgruppe getrennt auf Gruppenebene verglichen. Dies geschieht einerseits für die gesamte EG und KG sowie andererseits für jedes Level nach dem Modell von Fritz et al. (2013; 2018) getrennt, um die Wirksamkeit des EBM für verschiedene arithmetische Lernausgangslagen zu untersuchen. Um die Trainingseffekte des EBM mit denen der regulären Beschulung vergleichen zu können, werden die Lernzuwächse im Sinne der Differenz im Arithmetiktest zwischen erstem und zweiten Messzeitpunkt (gain scores) inferenzstatistisch verglichen. Zur Berechnung der entsprechenden Effektstärke wird der Empfehlung von Morris (2008) folgend die Formel nach Carlson und Schmidt (1999) verwendet. Abschließend wird für die EG der Einfluss von arithmetischem Vorwissen, Anzahl der Fördersitzungen sowie kognitiven und sprachlichen Fertigkeiten auf die mathematischen Leistungen zum zweiten Messzeitpunkt in einem Regressionsmodell ermittelt, um zu prüfen, inwiefern die Wirksamkeit des EBM von weiteren Einflussvariablen anhängt.
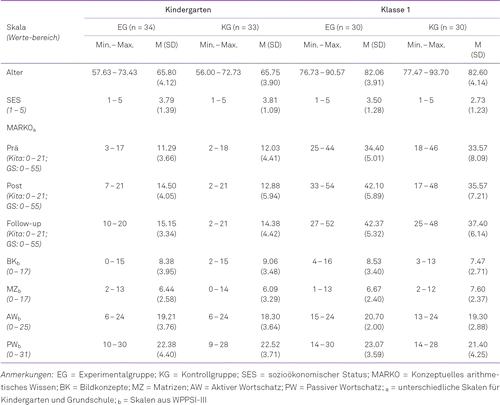
Sowohl im Kindergarten als auch in der Grundschule unterschieden sich Experimental- und Kontrollgruppe zum ersten Messzeitpunkt in Hinblick auf mathematisches Vorwissen, kognitive Fähigkeiten und Sprachstand nur geringfügig. Tabelle 1 bietet einen Überblick über die deskriptiven Statistiken der jeweiligen Gruppen. In paarweisen Vergleichen zum ersten Messzeitpunkt (t-Tests) zeigten sich bis auf eine Ausnahme keine signifikanten Unterschiede. In der ersten Klasse verfügten die Kinder der EG über einen signifikant besseren aktiven Wortschatz (t(58) = 2.187, p = .033, d = .29) als die Kinder der KG. Bei der Auswahl der Schulen und Kindergärten wurde im Vorfeld auf die Ausgeglichenheit der Einzugsgebiete geachtet. Da in allen Einrichtungen Kinder paritätisch in EG und KG aufgeteilt wurden, ist anzunehmen, dass sich die Kinder der EG und der KG nur unwesentlich hinsichtlich des sozialen und ökonomischen Umfeldes unterschieden. Auf eine präzise Messung des sozio-ökonomischen Status wurde mit Blick auf die zu erwartende Akzeptanz der Erziehungsberechtigten verzichtet.
Instrumente
Arithmetische Konzepte
Die arithmetische Konzeptentwicklung der Kinder wurde zu allen drei Messzeitpunkten (Prä-, Post-, Follow-up-Test) mit Tests erfasst, die auf dem Entwicklungsmodell nach Fritz et al. (2018) aufbauen. Im Kindergarten wurde der MARKO-S (Ehlert et al., 2020) eingesetzt, der die konzeptuelle Entwicklung bis zum dritten Level erfasst. In der ersten Klasse wurde die arithmetische Konzeptentwicklung mit dem MARKO-D (Ricken et al., 2013) gemessen, der die ersten fünf Level abdeckt. Wesentliche Gründe für die Verwendung zweier unterschiedlicher Tests waren erstens, dass im Kindergarten die unteren Levels von besonderer Bedeutung sind, insbesondere vor dem Hintergrund gezielter Intervention (Fritz et al., 2018). Zweitens beträgt die Durchführungsdauer des MARKO-D etwa 30 Minuten, die des MARKO-S hingegen nur etwa 10 Minuten. Die Testbedingungen im Kindergarten ließen einen Einsatz des zeitaufwändigeren MARKO-D nicht zu. Die Reliabilität beider Testverfahren ist akzeptabel bis gut (MARKO-S: Personenebene: r = .69, Itemenebene: r = .99; MARKO-D: r = .89). Für die Analysen wurden die Rohwerte verwendet.
Kognitive Fähigkeiten
Die kognitiven Fähigkeiten der Kinder wurden zum Prätest mit den Skalen „Bildkonzepte“ (BK) und „Matrizen“ (MZ) der Wechsler Preschool and Primary Scale of Intelligence – III (WPPSI-III) (Petermann, Ricken, Fritz, Schuck & Preuß, 2014) erfasst. Beide Subtests laden im Wesentlichen auf dem Testteil „Handlungsteil“, der den allgemeinen g-Faktor im Intelligenzmodell nach Cattell, Horn und Carrol abbildet (Petermann et al., 2014). Beim Subtest BK waren die Kinder gefordert, aus zwei Reihen mit je zwei bis drei Bildern ein Paar aus beiden Reihen zu finden, das eine Gemeinsamkeit besitzt. Die Gemeinsamkeiten waren kategorial (z.B. Musikinstrumente) oder funktional (z.B. das Objekt vergrößert). Der Subtest MZ erforderte die kreuzweise Klassifikation einer Vierfeldertafel nach zwei Kriterien (z.B. Form und Anzahl). Hierbei war eins der Felder leer und musste aus vier gegebenen Möglichkeiten vervollständigt werden. Die Skalen wiesen in der Validierungsstudie gute Reliabilitäten (BK: r = .80; MZ: r = .81) auf. Für die Analysen wurden die Rohwerte verwendet.
Sprachliche Fähigkeiten
Die sprachlichen Fähigkeiten der Kinder wurden im Prätest mit zwei Skalen – aktiver Wortschatz (AK) und passiver Wortschatz (PW) – aus der WPPSI-III erfasst. Die beiden Skalen laden vorwiegend auf dem Testteil „Verbalteil“. Beim Subtest AK wurden Bilder von Alltagsgegenständen gezeigt und nach deren Namen gefragt. Für alle Items lagen Zielantworten zur Bewertung vor. Beim Subtest PW erhielten die Kinder eine Vorlage mit vier Bildern, verbunden mit dem Auftrag auf ein bestimmtes Bild zu zeigen („Zeige auf den Ball“). Die Skalen wiesen in der Validierungsstudie akzeptable Reliabilitäten (AK: r = .78; PW: r = .74) auf. Für die Analysen wurden die Rohwerte verwendet.
Ergebnisse
Lernzuwächse durch adaptive Förderung mit dem EBM (Forschungsfragen 1 und 2)
Im Vergleich von Prä- und Posttest haben sowohl die Kinder in den Experimental- als auch die Kinder in den Kontrollgruppen Lernzuwächse auf Gruppenebene erzielt. Dabei sind für die beiden Experimentalgruppen (Kindergarten: t(33) = 4.824, p < .001, d = .84; Grundschule: t(29) = 11.526, p < .001, d = 2.14) stärkere Leistungszuwächse zu verzeichnen als für die beiden Kontrollgruppen (Kindergarten: t(32) = 1.020, p = .315, d = .18; Grundschule: t(29) = 2.515, p = .018, d = .47). Im direkten Vergleich der Leistungszuwächse (gain scores) vom ersten zum zweiten Messzeitpunkt zeigen sich im Kindergarten marginal signifikante Unterschiede zugunsten der EG (t(65) = 1.7207, p = .09) bei einer Effektstärke von d = .42. In der Grundschule sind die Lernzuwächse in der EG signifikant höher als in der KG t(58) = 5.4886, p < .001) bei einer Effektstärke von d = .85. Das Entwicklungsmodell nach Fritz et al. (2018) macht es möglich, die Lernzuwächse innerhalb der Levelsequenz zu quantifizieren. So haben im Kindergarten 55.9% der Kinder im Laufe der Förderphase das nächsthöhere Level erreicht. In der Grundschule betrug dieser Anteil 76.7%; 26.7% der Kinder in der ersten Klasse haben sogar zwei konzeptuelle Levels dazugewonnen.
Erwartungsgemäß verringern sich die Effekte von Interventionen nach deren Ende, sodass die individuellen Leistungen im Follow-up zumeist unter denen des Posttests bleiben (Aunio, Hautamäki & van Luit, 2005). Die positiven Effekte vieler Interventionen können demnach nur sehr bedingt nach deren Ende aufrechterhalten werden. Auch in der vorliegenden Studie sind die Lernzuwächse in den Experimentalgruppen beider Altersbereiche zwischen Posttest und Follow-up geringer (Kindergarten: t(26) = 1.140, p = .265, d = .22; Grundschule: t(29) = .352, p = .728, d = .07). Dementsprechend verringerten sich die Effekte der Intervention bezogen auf die Zeit von Prätest zu Follow-up, sind in der Grundschule jedoch noch im angestrebten Bereich (t(58) = 3.000, p < .01, d = .07, Grundschule: d = .61), im Kindergarten jedoch nicht mehr (t(65) = .587, p = .559, d = .22) (Hattie, 2009). Die Leistungen zu Prä-, Post- und Follow-up-Test sind ebenfalls in Tabelle 1 zusammengefasst.
Trainingseffekte in Abhängigkeit des arithmetischen Vorwissens (Forschungsfrage 3)
Das Training erfolgte adaptiv, d.h. die Spielvarianten wurden an die Lernvoraussetzungen der Kinder, hier das individuelle Level im Sinne des Modells von Fritz et al. (2018), angepasst. Um zu prüfen, inwieweit das EBM Trainingseffekte auf den verschiedenen Levels – und damit für alle Spielversionen – zeigt, wurden die Trainingseffekte für die Kinder auf den unterschiedlichen Levels einzeln betrachtet. Abbildung E6 im ESM1 veranschaulicht die Verläufe der Gruppen mit gleichem Level arithmetischer Konzepte zum Prätest über die drei Messzeitpunkte. In allen Subgruppen zeigen sich Leistungszuwächse innerhalb der Experimentalgruppe. Im Vergleich zu den jeweiligen Kontrollgruppen des gleichen Levels zeigen sich im Kindergarten auf den Levels I und II nicht signifikante, geringere Leistungszuwächse als in den Kontrollgruppen bei schwacher Effektstärke (t(10) = –.291, p = .777, d = –.31 und t(22) = –.532, p = .600, d = –.22). In den Subgruppen auf den Levels III und III + hingegen zeigen die Kinder der Experimentalgruppen zum Teil deutlich stärkere Leistungszuwächse auf als die Kinder der jeweiligen Kontrollgruppen, die allerdings nur für die Kinder auf Level III statistisch signifikant waren (t(24) = 2.391, p = .025, d = 3.51 und t(3) = 1.635, p = .201, d = .50). In der ersten Klasse sind die Ergebnisse hinsichtlich der Trainingseffekte auf den unterschiedlichen Levels konsistenter. Hier sind die Leistungszuwächse der Kinder aller Experimentalgruppen erheblich größer als bei den Kindern der Kontrollgruppen (d = .95, d = 2.99, d = 1.44 und d = 6.23) und in allen Vergleichen statistisch signifikant (p < .05für alle Vergleiche). Sowohl im Kindergarten als auch in der ersten Klasse zeigen sich damit für die Levels III bis V stärkere Trainingseffekte als in den Gruppen der Levels I und II. Bei der Betrachtung der Gruppenunterschiede in den Lernzuwächsen muss berücksichtigt werden, dass durch die teils sehr kleinen Teilstichproben die Aussagekraft der t-Tests eingeschränkt ist.
Auch für die Subgruppen mit gleichem arithmetischem Vorwissen lassen sich die Lernzuwächse im Rahmen des Entwicklungsmodells ausdrücken. Im Kindergarten haben auf Level I 50% der Kinder das nächsthöhere Level erreicht, auf Level II 33.3% und auf Level III 80%. Da hier mit dem MARKO-S nur die ersten drei Levels erfasst wurden, kann für die Gruppe auf Level III + keine entsprechende Aussage getroffen werden. In der ersten Klasse betrug der Anteil der Kinder, die das nächsthöhere Level erreichten auf Level II 100%, auf Level III 88.9%, auf Level IV 44.4% und auf Level V 66.7%. Einige Kinder in der Grundschule haben sogar das übernächste Level erreicht: Auf Level II waren dies 55.6%, auf Level III 11.1% und auf Level IV 22.2%.
Domänen-unspezifische Einflussfaktoren auf die Lernzuwächse durch das adaptive Training mit dem EBM (Forschungsfrage 4)
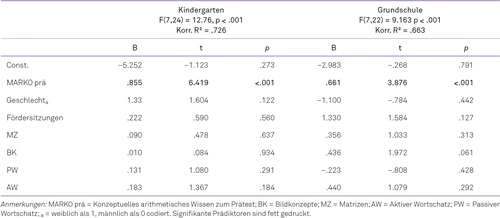
Um zu untersuchen, in welchem Maße die Trainingseffekte des EBM von individuellen Faktoren abhängen, wurde je ein Regressionsmodell für die beiden Experimentalgruppen aufgestellt. Die abhängige Variable bildete der Rohwert des Arithmetiktests zum Posttest. Unabhängige Variablen waren das individuelle mathematische Vorwissen zum Prätest, die Anzahl der erhaltenen Fördersitzungen sowie die kognitiven und sprachlichen Kontrollmaße zum ersten Messzeitpunkt. Die beiden Modelle sind in Tabelle 2 zusammengefasst. In beiden Modellen war erwartungsgemäß das individuelle arithmetische Vorwissen zum Prätest starker und signifikanter Prädiktor des arithmetischen Wissens zum Posttest. Die Anzahl der Fördereinheiten war entgegen den Erwartungen in beiden Modellen kein signifikanter Prädiktor für das arithmetische Wissen zum zweiten Messzeitpunkt. Das Geschlecht der Kinder sowie domänen-unspezifische kognitive und sprachliche Fertigkeiten waren ebenfalls keine signifikanten Prädiktoren.
Diskussion
Die vorliegende Studie verfolgte das Ziel, die Effektivität der spielbasierten Förderung mit dem EBM zu untersuchen. Die Ergebnisse zeigen, dass das EBM geeignet ist, das konzeptuelle arithmetische Wissen von Kindern im Kindergarten und der ersten Klasse zu steigern. Dabei hat sich die adaptive Förderung mit dem EBM, die sich am arithmetischen Vorwissen der Kinder orientiert, als wirksamer erwiesen als das freie Spielen im Kindergarten oder der mathematische Anfangsunterricht in der ersten Klasse. Dies zeigt sich in messbar größeren Lernzuwächsen der Kinder in den Experimentalgruppen. Einschränkend ist hierzu zu berichten, dass die Differenz der Lernzuwächse (gain scores) im Kindergarten für die gesamte Gruppe statistisch nur marginal signifikant waren (p = .09). Angesichts der Stichprobengrößen sollte das Signifikanzniveau nicht als ausschließliches Evaluationskriterium betrachtet werden. Die positiven Lerneffekte der Förderung mit dem EBM waren weitestgehend unabhängig von domänen-unspezifischen sprachlichen und kognitiven Faktoren, allerdings auch von der Anzahl der Fördereinheiten. Auch im Follow-up-Test nach drei Monaten blieben positive Effekte der Förderung mit dem EBM bestehen, wenngleich sie auch etwas geringer ausfielen. Diese Ergebnisse lassen sich als Hinweis auf längerfristige und nachhaltige Effekte der spielbasierten Förderung deuten.
Limitationen
Der Vergleich der Kindergruppen mit unterschiedlichem arithmetischem Vorwissen weist darauf hin, dass Kinder im gesamten Leistungsspektrum von der Förderung profitiert haben, jedoch nicht in gleichem Maße. Insbesondere haben die Kinder auf Level I und II von der Förderung mit dem EBM profitiert, ihre Lernzuwächse sind jedoch nicht substantiell größer als die der Kinder in den Kontrollgruppen. Eine mögliche Erklärung kann sein, dass diese Kinder offenbar erhebliche Schwierigkeiten mit dem (mathematischen) Lernen haben: Kinder auf Level I lernen gerade sicher zu zählen, Kinder auf Level II entwickeln erst eine Vorstellung von ordinalen Zahlbeziehungen. Damit bleiben diese Kinder in Hinblick auf ihre mathematische Entwicklung deutlich hinter ihren gleichaltrigen Peers zurück und sind den Anforderungen des mathematischen Anfangsunterrichts kaum gewachsen. Diese Kinder benötigen eine wesentlich intensivere Förderung mit einem evidenzbasierten Förderprogramm im Einzelsetting. Zu diesem Befund muss einschränkend erwähnt werden, dass durch die Aufteilung in Subgruppen mit gleicher Lernausgangslage die Stichprobengröße für die Analysen bezüglich Forschungsfrage 3 nur begrenzt verallgemeinerbar sind.
Bei näherer Betrachtung der Leistungsentwicklung der Kinder auf unterschiedlichen Levels fällt jedoch auf, dass die Leistungskurven der Kindergartenkinder auf Level I und II sowie auch der Grundschulkinder auf Level II nach dem Posttest relativ gradlinig weiter ansteigen, während die Leistungskurven der Kinder beider Gruppen auf den Levels III bis V abflachen. Mindestens zwei Erklärungen hierfür sind denkbar. Erstens greifen die Varianten des EBM auf den Levels I und II typische Lerninhalte auf, die im Kindergarten sowie der ersten Klasse vermittelt werden. Dazu gehören Zählkompetenzen, die vor allem im Kindergarten eine wesentliche Rolle spielen sowie ordinale Zahlkonzepte, die die Bestimmung der Nachbarzahlen, aber auch das zählende Lösen einfacher Additions- und Subtraktionsaufgaben ermöglichen (Fritz et al., 2018; Gelman & Gallistel, 1978; Le Corre, 2014). Damit werden die Lerninhalte, die für diese Gruppen relevant sind, im pädagogischen Alltag unterstützt und fortgeführt. Im Gegensatz dazu werden die Konzepte der Levels III bis V im Kindergarten sowie der ersten Klasse nur eingeschränkt vermittelt und wenn, dann eher implizit (z.B. in Ergänzungsaufgaben) thematisiert. Zweitens liegt der Schluss nahe, dass die Kinder auf Level I und II nur eher langsam mathematische Konzepte erwerben, wie sich aus ihren bereits bestehenden Wissensrückständen ableiten lässt. Diese Kinder benötigen daher mehr Zeit, um auf die Intervention zu reagieren, sodass sich größere Lerneffekte erst über einen längeren Zeitraum messen lassen.
Insgesamt waren die positiven Lerneffekte in der Grundschule höher als im Kindergarten. Auch hierfür lassen sich sinnvolle Erklärungen finden. Zum einen wurde im Kindergarten aus organisatorischen Gründen der MARKO-S zur Erfassung der mathematischen Lernzuwächse verwendet. Dabei handelt es sich in erster Linie um ein Screening, das daher weniger Items besitzt und folglich Lernzuwächse eventuell weniger präzise erfassen kann. Im Gegensatz dazu ist der in der ersten Klasse eingesetzte MARKO-D ein wesentlich umfangreicherer Test, der sensibler auf Leistungsveränderungen reagiert. Zum anderen sind die Lernstrukturen in der Grundschule viel formaler und die Kinder zur Mitte der ersten Klasse schon teilweise an formale Instruktionssettings wie spielbasierte Fördereinheiten gewöhnt. Im Gegensatz dazu geschieht das Lernen im Kindergarten oftmals eher informell. Die strukturellen Unterschiede in der Organisation von Lernen in Kindergarten und Grundschule kann mitursächlich für die unterschiedlichen Lerneffekte des EBM sein.
Implikationen für die Praxis
Während Kinder mit durchschnittlichem arithmetischem Vorwissen substantiell von der Förderung mit dem EBM profitieren, ist dessen Effektivität bei Kindern mit geringem arithmetischem Vorwissen weniger stark ausgeprägt. Gerade diese Kinder jedoch benötigen eine intensive Förderung. Vor dem Hintergrund dieser Befunde ist das EBM nur bedingt geeignet, eine intensive Förderung mit einem evidenzbasierten Förderprogramm zu ersetzen, bietet aber eine sinnvolle Möglichkeit, die Förderung arithmetischer Konzepte in Kindergarten und Grundschule zu unterstützen. Zum einen kann das EBM intensive Förderprogramme spielbasiert begleiten, indem es zusätzliche, adaptive Lerngelegenheiten während Spielzeiten, im offenen Ganztag oder gemeinsam mit den Eltern schafft. Zum anderen kann mit dem EBM individuelle Förderung auch für die Kinder bereitgestellt werden, die keine erheblichen Schwierigkeiten mit dem Rechnen haben. Für diese Kinder können angesichts anhaltend knapper zeitlicher und personeller Ressourcen im pädagogischen Alltag oftmals keine oder nur sehr wenige individuelle Förderangebote bereitgestellt werden. Darüber hinaus eignet sich das EBM besonders als Ergänzung in lerntherapeutischen Settings. Zur Vertiefung spezifischer Lerninhalte oder zum Ausklang einer Therapiestunde können spezifische Spielvarianten in förderlicher und zugleich motivierender Weise eingesetzt werden.
Die in der vorliegenden Studie berichteten positiven Effekte des EBM auf die arithmetische Konzeptentwicklung im Kindergarten und der ersten Klasse entstammen einer Studie, in der die individuelle Förderung mit dem EBM durch geschulte Studierende, also externen Förderkräften, durchgeführt worden ist. Die Befunde machen deutlich, dass es nicht ausreicht, das EBM als Spielangebot in Kindergarten oder Grundschule bereit zu halten und die Kinder zum gelegentlichen Spiel aufzufordern. Es entfaltet seine Wirkung vor allem dann, wenn die Spielvarianten adaptiv auf die individuellen Lernvoraussetzungen abgestimmt werden. Um einen Lernerfolg zu erzielen, sollten die Spiele auch kontinuierlich über einen längeren Zeitraum durchgeführt und im pädagogischen Alltag aufgegriffen werden.
In Hinblick auf die Implementation dieses Spielangebots für Kindergarten und Grundschule ist bekannt, dass sich Effekte von Interventionsstudien im Praxisfeld nur sehr eingeschränkt replizieren lassen (Aunio et al., 2005; Müller & Fritz-Stratmann, 2017). Wesentliche Schwierigkeiten bestehen hier einerseits darin, dass die pädagogischen Fachkräfte oftmals nicht ausreichend ausgebildet sind, eine zuverlässige Diagnostik zur Auswahl angemessener Spielvarianten vorzunehmen. Zudem fällt es ihnen oft schwer, eine kontinuierliche Förderung in den pädagogischen Alltag bzw. den Regelunterricht zu integrieren. Aber auch wenn diese Bedingungen nicht zuverlässig in allen Einrichtungen erfüllt werden können, sollte die Anwendung des EBM deswegen nicht unterbleiben. Kinder wählen bevorzugt diejenigen Spielvarianten, die ihrem Leistungsniveau entsprechen. Hierin sollten sie unterstützt und allmählich an die nächst schwierigeren Varianten herangeführt werden. Auf diese Weise können – auch unabhängig von einem therapeutischen Setting – durchaus positive Effekte erwartet werden.
Fazit
Zusammenfassend erweist das EBM als geeignetes Fördermaterial, um die Entwicklung frühen arithmetischen Wissens zum Schulanfang zu unterstützen. Der spielerische Elemente und ein Entwicklungsmodell vereinende Ansatz zeigt in Trainingseinheiten, die an das individuelle Vorwissen der Kinder angepasst sind, vor allem bei alterstypisch entwickelten Kindern substantielle Lerneffekte. Daher eignet sich das EBM vor allem als unterstützendes Material, kann aber als Lernspiel insbesondere bei Kindern mit erheblichen Lernrückständen intensive Förderprogramme nicht ersetzen.
Elektronische Supplemente (ESM)
Die elektronischen Supplemente sind mit der Online-Version dieses Artikels verfügbar unter https://doi.org/10.1024/2235-0977/a000358.

Literatur
(2013). Core knowledge and working memory as prerequisites of early school arithmetic. South African Journal of Childhood Education , 3 (1). https://doi.org/10.4102/sajce.v3i1.29
(2007). Number development and developmental dyscalculia. Developmental Medicine & Child Neurology , 49 (11), 868–873. https://doi.org/10.1111/j.1469-8749.2007.00868.x
(2010). Predicting children's mathematical performance in grade one by early numeracy. Learning and Individual Differences , 20 (5), 427–435. https://doi.org/10.1016/j.lindif.2010.06.003
(2005). Mathematical thinking intervention programmes for preschool children with normal and low number sense. European Journal of Special Needs Education , 20 (2), 131–146.
(1999). Impact of experimental design on effect size: Findings from the research literature on training. Journal of Applied Psychology , 84 , 851–862.
(2015). Interventions for Children With Mathematical Difficulties: A Meta-Analysis. Zeitschrift Für Psychologie , 223 (2), 129–144. https://doi.org/10.1027/2151-2604/a000211
(2019).
Subitizing: The Neglected Quantifier . In A. Norton M. W. Alibali (Eds.), Constructing Number (pp. 13–45). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-00491-0_2(1988). Children's initial understandings of ten. Focus on Learning Problems in Mathematics , 10 (3), 1–26.
(2013). Der Zahlensinn oder Warum wir rechnen können . Springer-Verlag.
(2009). Classification, Seriation, and Counting in Grades 1, 2, and 3 as Two-Year Longitudinal Predictors for Low Achieving in Numerical Facility and Arithmetical Achievement? Journal of Psychoeducational Assessment , 27 (3), 252–264. https://doi.org/10.1177/0734282908330588
(2016). Place-value understanding in number line estimation predicts future arithmetic performance. British Journal of Developmental Psychology , 34 (4), 502–517. https://doi.org/10.1111/bjdp.12146
(2005). Early Identification and Intervention for Students With Mathematics Difficulties. Journal of Learning Disabilities , 38 (4), 324–332. https://doi.org/10.1177/00222194050380040801
(2020). Mathematik-und Rechenkonzepte im Vorschulalter–Screening (MARKO-Screening). Göttingen: Hogrefe .
(2017). Diagnostik und Förderung bei Rechenschwäche: Messen wir, was wir fördern wollen? Lernen und Lernstörungen , 6 , 25–38. https://doi.org/10.1024/2235-0977/a000160
(2018). Arithmetische Konzepte aus kognitiv-entwicklungspsychologischer Sicht. Journal für Mathematik-Didaktik , 39 (1), 7–41. https://doi.org/10.1007/s13138-018-0131-6
(2013). Development of mathematical concepts as basis for an elaborated mathematical understanding. South African Journal for Childhood Education , 3 (1), 38–67.
(1988). Children's Counting and Concepts of Number. New York: Springer.
(2007). Rechenschwäche vorbeugen: Das Handbuch für LehrerInnen und Eltern . Öbv & hpt.
(2010). Elementare mathematische Bildung im Alltag der Kindertagesstätte: Grundlegung und Evaluation eines kompetenzorientierten Förderansatzes . Münster: Waxmann Verlag.
(1978). The child's understanding of number . Harvard University Press.
(2019). Welche Rolle spielen sprachliche Parameter für die Entwicklung integrierter verbal-numerischer Konzepte im vierten Lebensjahr? Frühe Bildung , 8 (1), 44–52. https://doi.org/10.1026/2191-9186/a000410
(2009). Visible Learning . London: Routledge.
(2019). Kindergarten children's symbolic number comparison skills relates to 1st grade mathematics achievement: Evidence from a two-minute paper-and-pencil test. Learning and Instruction , 59 , 21–33. https://doi.org/10.1016/j.learninstruc.2018.09.004
(2019).
Development of a Sustainable Place Value Understanding . In A. Fritz V. G. Haase P. Räsänen (Eds.), International Handbook of Mathematical Learning Difficulties (pp. 561–579). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-97148-3_33(2018). Erdmännchen-Blitzblick-Memo . Köln: Prolog.
(1994). A Mental Model for Early Arithmetic . 13.
(2014). Spielorientierte Förderung numerischer Kompetenzen im Vorschulalter und deren Eignung zur Prävention von Rechenschwierigkeiten . 18 .
(2013). Alltagsintegrierte Förderung numerischer Kompetenzen im Kindergarten. Frühe Bildung , 2 (2), 84–91.
(2009). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year longitudinal study. Learning and Instruction , 19 (6), 513–526. https://doi.org/10.1016/j.learninstruc.2008.10.002
(2019). Arithmetische Kompetenz und Rechenschwäche am Ende der Grundschulzeit: Die Rolle statusdiagnostischer undlernverlaufsbezogener Prädiktoren . 23 .
(2012). Non-numerical and Numerical Understanding of the Part-Whole Concept of Children Aged 4 to 8 in Word Problems. Journal Für Mathematik-Didaktik , 33 (2), 233–262. https://doi.org/10.1007/s13138-012-0039-5
(2014). Children acquire the later-greater principle after the cardinal principle. British Journal of Developmental Psychology , 32 (2), 163–177. https://doi.org/10.1111/bjdp.12029
(2007). One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition , 105 (2), 395–438. https://doi.org/10.1016/j.cognition.2006.10.005
(2015). Learning pathways within the multiplicative conceptual field: Insights reflected through a Rasch measurement framework . Münster: Waxmann Verlag.
(2014). Number and counting skills in kindergarten as predictors of grade 1 mathematical skills. Learning and Individual Differences , 34 , 12–23. https://doi.org/10.1016/j.lindif.2014.05.006
(2008). Estimating Effect Sizes From Pretest-Posttest-Control Group Designs. Organizational Research Methods , 11 (2), 364–386. http://doi.org/10.1177/1094428106291059
(2017). Implementation des Trainingsprogrammes Kalkulie in der Grundschule. Lernen und Lernstörungen , 6 , 7–17. https://doi.org/10.1024/2235-0977/a000158
(2014). Wechsler Preschool and Primary Scale – Third edition. Deutschsprachige Adaption nach D. Wechsler . Göttingen: Hogrefe.
(1983).
A Developmental Theory of Number Understanding . In H. Ginsberg (Hrsg.), The Development of Mathematical Thinking (S.109–151). New York: Academic.(2013). MARKO-D: Mathematik- und Rechenkonzepte im Vorschulalter-Diagnose: Mit Ergänzungstest Konventions- und Regelwissen . Göttingen: Hogrefe.
(2005). Children's thinking ( 4th ed ). Upper Saddle River, N.J: Pearson Education/Prentice Hall.
(2008). Playing linear numerical board games promotes low-income children's numerical development. Developmental Science , 11 (5), 655–661. https://doi.org/10.1111/j.1467-7687.2008.00714.x
(2019).
Counting and Basic Numerical Skills . In A. Fritz V. G. Haase P. Räsänen (Eds.), International Handbook of Mathematical Learning Difficulties (pp. 521–542). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-97148-3_31(2013).
Vorschulische Förderung im Kindergartenalltag . In G. Faust (Hrsg.), Einschulung – Ergebnisse aus der Studie „Bildungsprozesse, Kompetenzentwicklung und Selektionsentscheidungen im Vorschul- und Schulalter (BiKS)“ (S.69–82). Münster: Waxmann.(2014). The emergence of “groupitizing” in children's numerical cognition. Journal of Experimental Child Psychology , 126 , 120–137. https://doi.org/10.1016/j.jecp.2014.03.006
(1992). Schemes of action and operation involving composite units. Learning and Individual Differences , 4 (3), 259–309. https://doi.org/10.1016/1041-6080(92)90005-Y
(1998). Die Entwicklung des mathematischen Verständnisses im Kindesalter . Pabst Science Publishers.
(2010). How 15 Hundred Is Like 15 Cherries: Effect of Progressive Alignment on Representational Changes in Numerical Cognition: Effect of Progressive Alignment. Child Development , 81 , 1768–1786. https://doi.org/10.1111/j.1467-8624.2010.01509.x
(1992). Children's acquisition of the number words and the counting system. Cognitive Psychology , 24 (2), 220–251. https://doi.org/10.1016/0010-0285(92)90008-P