Entwicklung und Evaluation eines Screening-Verfahrens zur Prognose von Rechenschwierigkeiten in der Grundschule
Das Flensburger Schulspiel (FleSch)
Abstract
Zusammenfassung.Hintergrund: Einen wichtigen Baustein im Rahmen der Prävention von Rechenschwierigkeiten stellen Screening-Verfahren dar, die ein individuelles Entwicklungsrisiko zuverlässig und frühzeitig aufzeigen. Die meisten Instrumente zur Prognose solcher Schwächen im Grundschulalter sind überwiegend als vergleichsweise zeitaufwändige Einzelverfahren konzipiert. Das Ziel der vorliegenden Studie ist die Entwicklung und Evaluation eines gruppenbasierten Screening-Verfahrens für den Einsatz am Schulanfang. Methode: Im vorliegenden Beitrag werden die Entwicklung und Evaluation eines Filter-Screenings an einer Stichprobe von insgesamt 174 Erstklässlern beschrieben. Ein breites Variablen-Set aus domänenspezifischen und domänenunspezifischen Prädiktoren der mathematischen Leistung wurde in die Analyse einbezogen. Resultate: Auf der Basis der logistischen Regressionsanalyse konnte ein durch eine Kreuzvalidierung abgesichertes Vier-Variablen- Prognosemodell (Mengenschätzen, Vorgänger benennen, Zahlen lesen, Matrizen-Test) identifiziert werden, das sehr gute AUC-Werte (bis zu >> .90) aufweist. Diskussion: Die Ergebnisse liefern wertvolle Erkenntnisse hinsichtlich der Implementation eines validen und Schuleingangsscreenings als Gruppenverfahren.
Abstract.Background: Screening tools aiming at detecting preschool children at risk for developing arithmetic difficulties play an important role in preventing poor mathematic achievement. However, existing instruments are designed for individual administration which is rather time-consuming. The aim of the present study was to develop and evaluate a group-administered numerical screening instrument for children entering primary school. Methods: Overall, 174 first graders participated in the study. A large set of domain-specific and domain-unspecific predictor variables were entered into the data analyses. Results: On the basis of a logistic regression analysis, a four-variable prognosis model (estimating quantities, naming predecessors, reading numbers, matrix test), secured by a cross-validation, could be developed, which deliver very good AUC- values (up to >> .90). Discussion: The results provide valuable findings for an implementation of a screening procedure for children entering primary school.
Einleitung
Das Erlernen eines mathematischen Verständnisses sowie arithmetischer Grundfertigkeiten gehören zu den zentralen Entwicklungsaufgaben in der Grundschule. Für Rechenstörungen finden sich in Abhängigkeit von zugrundeliegenden Diagnosekriterien Prävalenzraten zwischen 3 und 8% (Shalev, Auerbach, Manor & Gross-Tsur, 2000; von Aster, Schweiter & Weinhold-Zulauf, 2007), wobei die Auftretenswahrscheinlichkeit einer Rechenschwäche im Grundschulalter weitaus höher liegen dürfte, wenn Schülerinnen und Schüler einbezogen werden, die das intelligenzabhängige Doppeldiskrepanz-Kriterium nicht erfüllen (Fischbach et al., 2013). Unabhängig davon zeigt sich für die betroffenen Schülerinnen und Schüler eine ungünstige Prognose, die zudem um so ungünstiger auszufallen scheint, je später die Schwierigkeiten diagnostiziert wurden (Kohn, Wyschkon, Ballaschk, Ihle & Esser, 2013; Schulz et al., 2018; Shalev, Manor & Gross-Tsur, 2005). Das damit verbundene enorme Entwicklungsrisiko infolge verpasster Fördermöglichkeiten bezeichnet die bekannte wait-to-fail-Problematik (Vaughn, Vaugh & Fuchs, 2003), in der gravierende Schwierigkeiten und Komorbiditäten erst eskalieren müssen, bevor notwendige Maßnahmen einsetzen (Huber & Grosche, 2012). Demgegenüber wird mit dem Response-to-Intervention (RTI)-Ansatz ein konsequent präventiver Umgang mit Lernschwierigkeiten im Sinne einer frühen Identifikation, Prävention und Intervention bei Lern- und Verhaltensproblemen gefordert. Einer frühzeitigen und validen Risikoabschätzung durch Filterscreenings sollten notwendigerweise eine weiterführende Diagnostik sowie gezielte Fördermaßnahmen folgen (Fuchs & Fuchs, 1986; Huber & Grosche, 2012, Reschley & Bergstrom, 2009; Tröster, 2009; Walter, 2008). Ziel des vorliegenden Artikels ist es, ergänzend zum genannten RTI-Ansatz durch die Präsentation von ersten Evaluationsbefunden eines neu entwickelten Screening-Verfahrens, dem Flensburger Schulspiel (FleSch, Walter & Clausen-Suhr i.V.), einen Beitrag bezüglich der Entwicklung von Filterscreenings zu leisten. Das genannte Instrument wurde abweichend von vorhandenen sehr ressourcenintensiven und daher wenig praktikablen Einzelverfahren ressourcenschonend als Gruppenverfahren konzipiert.
Spezifische und unspezifische Prädiktoren der Rechenfähigkeit und Entwicklung des mathematischen Denkens
Zur Erklärung von Unterschieden in der Mathematikleistung werden sowohl domänenspezifische als auch dömänenunspezifische Teilfertigkeiten herangezogen (Abb. 1), wobei deren Gewichtung und präzise Auswahl uneinheitlich ausfallen (von Aster, Kucian, Schweiter & Martin, 2005; von Aster et al., 2007).
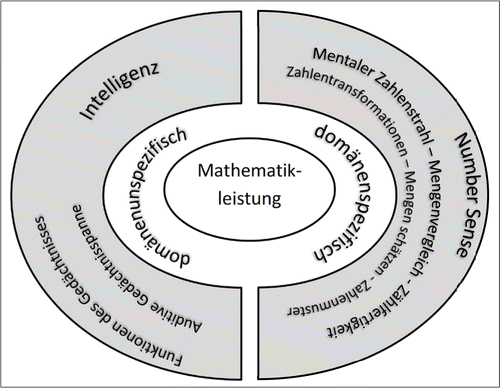
In den letzten zwei Jahrzehnten rückte zunehmend die Bedeutung spezifischer mathematischer Vorläuferfertigkeiten unter dem Konzept des Number Sense mit unterschiedlichen Operationalisierungen in den Mittelpunkt (Aunio et al., 2006; Berch, 2005; Gersten, Jordan & Flojo, 2005): Angefangen von der Definition des Number Sense als angeborene Fähigkeit zur Unterscheidung von Mengen, von der ausgehend sich eine komplexere Zahlverarbeitung im Sinne eines inneren mentalen Zahlenstrahls entwickelt (Dehaene, 1992), über die Zählkompetenz (Eins-zu-Eins-Korrespondenz, Kardinalitätsprinzip, Zählen, Vorgänger und Nachfolger benennen), das Zahlenwissen (Vergleichen von Mengen und numerischen Größen), die Transformation von Zahlen (Addition und Subtraktion, Rechnen), das Schätzen von Mengen und das Erkennen von Zahlenmustern (Jordan, Kaplan, Oláh & Lokuniak, 2006; Lambert, 2015) bis hin zur Fähigkeit zur Verknüpfung von Beziehungen und Rechenprinzipien (Berch, 2005; Lambert, 2015). Mehrfach konnte die prädiktive Bedeutung früher Zählkompetenzen im Vorschulalter belegt werden (Aunola, Leskinen, Lerkkanen & Nurmi, 2004; Koponen, Aunola, Ahonen & Nurmi, 2007; Passolunghi, Vercelloni und Schadee, 2007; Zhang et al., 2020). Andernorts erbrachten breitere Variablen-Sets (Zählfertigkeiten, Zahlwissen, Vorgänger, Nachfolger, Vergleiche, nonverbales Rechnen, Addition und Subtraktion, Zahlzerlegung) die beste Prognoseleistung (Jordan, Kaplan, Locuniak und Ramieni, 2007; Jordan, Kaplan, Ramineni & Lokuniak, 2009). Mazzocco & Thompson (2005) wiesen auf eine überlegene Bedeutung numerischer Basiskompetenzen gegenüber allgemein-kognitiven Variablen hin. Sie entwickelten darüber hinaus auf der Grundlage von Einzelitems Prognosemodelle (Invarianz, Mengenbeurteilung, Rückwärts zählen, einfache Addition, Zahlenlesen) mit einer noch größeren Gesamttrefferquote als die Modellierung auf Grundlage der Untertest-Summenwerte. Dabei erhielten unterschiedlich schwierige Items derselben Skala Zählfähigkeit auch unterschiedliche Gewichte: Während das Rückwärtszählen den größten Beitrag zur Steigerung der Prognosegüte leistete, konnte das Abzählen von Mengen kleiner fünf die Gruppe der rechenschwachen und nicht-rechenschwachen Kinder nicht trennen.
Die Ergebnisse sind deshalb von großem Interesse für die Thematik, weil hier eine Prognose auf Item-Ebene modelliert wurde. In der Modellierung der in der Erziehungswissenschaft häufig vorkommenden latenten Konstrukte werden in der Mehrzahl reflektive Messmodelle herangezogen (Ebert & Raithel, 2009; Fluck, 2020), die davon ausgehen, dass bestimmte Indikatoren (Items) ein nicht beobachtbares Konstrukt widerspiegeln. Das Konstrukt ist den Indikatoren damit kausal vorgeordnet. Steigt die Leistung in einem Konstrukt, so ist die Wahrscheinlichkeit größer, dass ein Einzelitem gelöst wird. Eine hohe Korrelation der Einzelitems ist eine Modellvoraussetzung und der Wert des Konstrukts wird über die Summenbildung gleichwertiger Items erreicht (Eberl, 2004; Fluck, 2020). Demgegenüber werden Indikatoren (Items) in formativen Messmodellen als distinkte Aspekte des latenten Konstrukts verstanden, die nicht untereinander austauschbar sind und damit die Voraussetzung entfällt, dass diese miteinander korrelieren. Vor dem Hintergrund der Befunde von Mazzocco & Thompson (2005) erscheint es lohnend, Prädiktoren zur Vorhersage von Rechenschwierigkeiten einer Modellierung auf der Grundlage eines formativen und damit itembasierten Messmodells zu unterziehen. Die Betrachtung unterschiedlicher Messmodelle mag auf den ersten Blick recht theoretisch anmuten. Tatsächlich ist es aber so, dass die Entscheidung für ein Messmodell im Rahmen der Datenanalyse, gerade auch wenn es um die Prognose von Ereignissen oder Zuständen und das Aufdecken individueller Unterschiede geht, durchaus unterschiedliche Befunde hervorbringen kann.
Genau dies zeigten Seeboth & Mõttus (2018) in einer groß angelegten Studie im Rahmen der Persönlichkeitsforschung (N = 8719). Sie fanden, dass itembasierte Modelle (formatives Messmodell) gemittelt über alle Outcomes (R2 = .0545) über eine um 61% bessere prognostische Kraft verfügten als Modelle, in denen dieselben Items in aggregierter Form (Domänen-Modelle) in ein Regressionsmodell eingegeben wurden (R2 = .0335). Erklärt werden die Befunde u.a. damit, dass Items aus Persönlichkeitsfragebögen hoch spezifische Informationen beinhalten, die durch die Aggregation zu einem Summenwert verloren gehen und damit die Erfassungsinstrumente an Prognosekraft verlieren.
Im deutschsprachigen Raum lassen sich ähnliche Befundmuster zur Früherkennung mathematischer Leistungen erkennen. Krajewski (2008) untersuchte den Einfluss früher mathematischer Kompetenzen im Bereich des Mengen- und Zahlenwissens auf die spätere Mathematikleistung. Während sich zusätzlich berücksichtigte unspezifische Prädiktoren besonders zu Beginn für den Aufbau grundlegender Zahlen- und Mengenvorstellungen einflussreich zeigten, überwog die prädiktive Aussagekraft des frühen Mengen- und Zahlenwissens zur Vorhersage der Mathematikleistungen am Ende der ersten, zweiten sowie der vierten Klasse und war bis in das neunte Schuljahr hinein nachweisbar (Krajewski, 2008; Krajewski & Schneider, 2006; Krajewski & Ennemoser, 2013).
Insgesamt erscheint die besondere Bedeutung domänenspezifischer Prädiktoren der Mathematikleistung belegt (von Aster et al., 2007). Darüber hinaus wird jedoch auch deutlich, dass nach der Kategorisierung von Geary (2007) als primäre Basiskompetenzen bezeichnete allgemein-kognitive Funktionen, insbesondere Funktionen des Arbeitsgedächtnisses und der Intelligenz, einen weiteren Anteil zur Steigerung der Prognose von Schulleistungen ausmachen (Geary, 2011; Geary, Bailey & Hoard, 2009; Knievel, Daseking & Petermann, 2010). So berücksichtigen beispielsweise auch von Aster et al. (2005) in ihrem neuropsychologisch basierten Entwicklungsmodell der Zahlenverarbeitung die Kapazität des Arbeitsgedächtnisses als limitierenden Faktor einer gelingenden Entwicklung. Zahlreiche Befunde deuten auf die Bedeutung der auditiven Gedächtnisspanne als Beitrag zur Vorhersage der Mathematikleistung hin (Alloway & Alloway, 2010; Dornheim, 2008; Passolunghi et al., 2007). Befunde bezüglich der prädiktiven Bedeutung der Intelligenz fallen in Abhängigkeit vom Entwicklungsalter, dem Prognosezeitraum und der Definition des vorherzusagenden Kriteriums uneinheitlich aus. So fanden Krajewski und Schneider (2009), dass die prognostische Wirkung gegen Ende der Grundschulzeit nur noch indirekt feststellbar ist, während Geary, Nicholas, Li & Sun, (2017) eine Zunahme der prognostischen Bedeutung der Intelligenz bei komplexeren mathematischen Aufgaben am Ende der Grundschulzeit fanden. In höheren Klassenstufen wiederum scheinen mathematische Kompetenzen in der 2. Klasse der Grundschule die Bedeutung der Intelligenz als Prädiktor zu übertreffen (Stern, 2013).
Screening-Verfahren in der Schuleingangsphase und ihre prognostische Validität
Screening-Verfahren erfüllen nicht die Aufgabe, eine umfassende Diagnose zu liefern, aus der geeignete Interventionsmaßnahmen ableitbar wären, sondern sie haben als diagnostische Instrumente eine Filterfunktion, um bei einem positiven Befund eine Risikoabschätzung vorzunehmen, an die sich weitere diagnostische Erhebungen anschließen (Tröster, 2009, S. 69).
Das binär logistische Regressionsmodell ist deshalb dem linearen Regressionsmodell für die Evaluation von Screening-Modellen vorzuziehen (Catts, Nielsen, Bridges, Liu & Bontempo, 2015), weil sich dadurch Wahrscheinlichkeitsaussagen bezüglich eines dichotom definierten Kriteriums auf der Grundlage der gegebenen miteinander linear kombinierten unabhängigen Prädiktoren schätzen und sich daraus Güte-Indizes zur Beurteilung eines Screening-Verfahrens ermitteln lassen (Backhaus, Erichson, Plinke & Weiber, 2018; Tröster, 2009). Zentral sind dafür die Sensitivität (SN) und die Spezifität (SP), der prävalenzunabhängige Youden-Index (YI) kann als Kennwert für die Trennschärfe herangezogen werden. Die positive (PK) und negative Korrektheit (NK) werden als Maß für die Sicherheit eines Verfahrens angegeben. Schließlich bezeichnet der RATZ-Index die generelle Leistungsfähigkeit eines Screenings und sollte über 66% liegen (Jansen, Mannhaupt, Marx & Skowronek, 2002).
Um die Beziehung von Sensitivität und Spezifität bei allen denkbaren Risiko-Cutoffs zur Vorhersagegüte des Modells zu nutzen, werden oftmals ROC-Analysen berechnet, die eine gewisse Fläche (AUC, Area Under the Curve) unter der ROC-Kurve definieren. AUC-Werte von größer als 0.80 sprechen für ein gutes Prognosemodell, Werte größer als .90 gelten als hervorragend (Backhaus et al., 2018; Catts et al., 2015; Tröster, 2009).
Verfügbare Screening-Verfahren im mathematischen Bereich sind in den vergangenen Jahren vorwiegend als Einzeltests entwickelt worden, deren Durchführung mit Schulanfängern eines kompletten Jahrgangs extrem viel Zeit und Personal erfordern, was eine fehlende Akzeptanz seitens der Praxis und den notwendigen flächendeckenden Einsatz erschweren dürfte. Zudem fällt bedauerlicherweise die Vorhersage-Güte mit RATZ-Werten unter 50% oftmals nicht zufriedenstellend aus (Gomm, 2014; Walter, 2016a, Walter, 2020). Demgegenüber konnte jedoch in einschlägigen Vorarbeiten (Walter, 2016b, Walter, 2020)ein Screening-Tool entwickelt werden, das auf der Grundlage der 18 Untertests der ZAREKI- K (von Aster, Bzufka & Horn, 2009) nach dem Verfahren der schrittweisen logistischen Regression ein Variablen-Set aus 6 Untertests (Vorwärtszählen, Vorgänger/Nachfolger benennen, Text-/ Sachaufgaben, Visuelles Rechnen, Zahlerhaltung und Zahlen schreiben) umfasst und beim Einsatz am Anfang der ersten Klasse (N = 396, AUC = .89, RATZ-Wert = 74.6%, p (y = 1) ≥ .192) 90 Prozent der Kinder richtig klassifizieren konnte. Die Reduzierung der Anzahl der Untertests ging also nicht mit einer Verschlechterung des Prognosemodells einher. In einer Teilstichprobe dieser Studie konnte die nichtsprachliche allgemeine Intelligenz, gemessen mit dem CFT-1 (Catell, Weiß & Osterland, 1997) das Prognosemodell nicht verbessern (Walter, 2020).
Einen ähnlichen Anspruch auf die Entwicklung eines zeitökonomisch einsetzbaren Instruments erhoben Jordan, Glutting & Ramineni (2010), die mit dem verkürzten Number Sense Brief (NSB) die Aufgabenklassen auf die Bereiche Zahlenfolge, Anzahlkonzept und -vergleich, Zahlenzusammensetzung, Textaufgaben und Anzahldifferenzen reduzierten. Das Kurz-Screening wurde zu Beginn der ersten Klasse mit einer guten Prognoseleistung für die zweite Klassenstufe eingesetzt. Die Aufgabenklassen des bei Walter (2016 b; 2020) ermittelten reduzierten Variablen-Sets weisen zu den Aufgabenklassen von Jordan, Glutting & Ramineni,(2010) durchaus erkennbare Überschneidungen auf.
Die Konzeption der Diagnoseaufgaben im Flensburger Schulspiel basieren auf Vorbefunden zur Prognosegüte der ZAREKI-K (Walter, 2016a, Walter, 2020), deren theoretische Konzeption daher für diesen Beitrag von besonderem Interesse ist. Die Testbatterie ZAREKI-K basiert auf einem vierstufigen neuropsychologisch ausgerichteten Entwicklungsmodell in drei unterschiedlichen Zahlenrepräsentationen unter Berücksichtigung der Arbeitsgedächtniskapazität (von Aster et al., 2005). Unter Beteiligung der Arbeitsgedächtnisleistung werden angeborene Kompetenzen des „Zahlensinns“ als primäre Ausprägungsform des mentalen, jedoch in früher Entwicklungsphase noch an die konkrete Anschauung gebundenen Zahlenstrahl, durch instruktions- und umweltabhängige Einflussfaktoren und die Aktivierung der sprachlich-auditiven und visuell-arabischen Zahlverarbeitung zu einem inneren mentalen (und von der konkreten Anschauung losgelösten) Zahlenstrahl modularisiert. Je besser diese drei Repräsentationsebenen von Zahlen durch eine Vielzahl gelingender Transkodierungsprozesse miteinander verknüpft werden, desto eher ist von einer ungestörten Zahlenverarbeitung auszugehen. Entwicklungsrisiken ergeben sich aus diesem Modell damit sowohl im Bereich der angeborenen neuronalen Netzwerke als auch im Bereich der instruktionsabhängigen Erwerbsprozesse (von Aster, 2005).
Fragestellung und Zielsetzung
Im Folgenden sollen erste Befunde zur Evaluation des neu entwickelten Gruppen-Screening-Verfahrens Flensburger Schulspiel (FleSch) hinsichtlich seiner klassifikatorisch-prognostischen Validität für die Rechenleistung am Anfang der zweiten Klasse untersucht werden. Maßgeblich in der Entwicklung des Flensburger Schulspiels war es, ein Gruppenverfahren zu entwickeln, das zeitökonomisch einsetzbar, damit praktikabel und ressourcenschonend eingesetzt werden kann und zugleich den geforderten Gütekriterien vollumfänglich gerecht wird. Die Konstruktion der Subtests und Items erfolgten auf Grundlage der dargelegten Befundlage sowie der dargestellten theoretischen Verankerung der Testkonstruktion der ZAREKI-K.
- 1.Es sollte zunächst geklärt werden, ob sich aus einem zunächst breit angelegten Set aus domänenspezifischen und domänenunspezifischen Prädiktor-Variablen ein gutes bis sehr gutes Prognosemodell zur Risikoabschätzung einer Rechenschwäche bilden lässt.
- 2.In einem zweiten Schritt sollte der Frage nachgegangen werden, ob auch auf Grundlage eines reduzierten Prädiktoren-Modells eine gleich gute Risikoabschätzung möglich wird. Dabei wurde erwartet, dass auch durch eine reduzierte Anzahl von Prädiktoren eine Klassifikation von Kindern mit und ohne Risikostatus bezüglich ihrer zukünftigen Rechenleistung – auch unter Einbeziehung allgemein-kognitiver Kompetenzen- zuverlässig erreicht werden kann.
- 3.Des Weiteren sollte geprüft werden, inwiefern ein formatives Messmodell auf Item-Ebene dem sonst üblichen reflektiven Modell hinsichtlich der klassifikatorisch-prognostischen Validität überlegen ist.
- 4.Schließlich interessierte, ob das hier entwickelte Screening-Verfahren die geforderten Güte-Indizes zur Vorhersage von Rechenschwierigkeiten erfüllen kann. Besondere Berücksichtigung sollte dabei ein Vergleich der Güte-Indizes zur Klassifikation von Risikokindern auf der Basis des reflektiven gegenüber dem formativen Modell finden. Es wird vermutet, dass die Bestimmung der Klassifikationsgüte nach der Modellierung auf Itemebene bessere Ergebnisse liefert.
Methode
Stichprobe
In der ersten Evaluationsphase des Flensburger Schulspiels konnten Vorläuferfertigkeiten von N = 258 Kindern aus 12 Grundschulen etwa sechs bis acht Wochen nach Beginn des ersten Schuljahres (Testzeitpunkt 1 im Oktober/November 2019) erhoben werden. Die Schülerinnen und Schüler der ersten Klasse, davon 135 Jungen (52.3%) und 123 Mädchen (47.7%), waren zum ersten Messzeitpunkt im Alter von 73 bis 105 Monaten (MW = 85.3, SD = 5.5). Insgesamt N = 21 Schülerinnen und Schüler (8.1%) kamen aus Haushalten, in denen neben Deutsch eine weitere Sprache gesprochen wurde, 7 Kinder (2.7%) besaßen einen förmlich festgestellten sonderpädagogischen Förderbedarf. Die Überprüfung der Mathematikleistung mit dem DEMAT 1+ (Krajewski, Küspert & Schneider, 2002) schloss sich im Abstand von einem knappen Jahr zu Beginn des zweiten Schuljahres (Testzeitpunkt 2 im Mai/Juni2020) an. Die Anzahl von N = 184 Kindern der Ausgangsstichprobe konnte mit einer mittleren Leistung (DEMAT-gesamt) von T = 47.7 (SD = 11.9) in die Kriteriumsmessung einbezogen werden. Gründe für den Dropout vom ersten zum zweiten Messezeitpunkt waren pandemiebedingte organisatorische Schwierigkeiten, Krankheit und Umzug der teilnehmenden Schülerinnen und Schüler oder vor allem unvollständige Datensätze über zwei Messzeitpunkte bedingt durch Testabbrüche oder Störungen während der Testdurchführung. Die Prävalenz rechenschwacher Schülerinnen und Schüler lag zu Beginn der zweiten Klasse mit N = 50 (19.4%, PR ≤ 25), N = 42 (16%, PR ≤ 16) und N = 31 (12%, PR ≤ 10) knapp im zu erwartenden Bereich und tendenziell erhöht. Anzumerken bleibt, dass in dem Untersuchungszeitraum es teilweise zu Distanzunterricht infolge pandemiebedingter Schulschließungen kam, die jedoch in allen beteiligten Klassen in gleichem Umfang zum Tragen kamen.
Vorgehensweise
Um eine altersangemessene Form der Testdurchführung zu erreichen, die möglichst bei allen Kindern die notwendige Motivation und Aufmerksamkeit erreicht, wurden die Untertests in eine Rahmenhandlung eingebettet, die in Form eines Stationsverfahrens zusätzlich Bewegungspausen, musische Elemente und ein kontinuierliches Kontingenzmanagement vorsieht. Angeleitet durch eine Handpuppe (Friedel Fuchs, der für seine Aufnahme in die Fuchsschule verschiedene Aufgaben kennenlernen und dem strengen Schulleiter am Ende vorweisen muss) durchlaufen die Schülerinnen und Schüler an den Stationen Untertests, in denen jeweils unterschiedliche Protagonisten in die Aufgabenstellung einführen. An den Übergängen von Station zu Station werden Bewegungsaufgaben innerhalb der Rahmenhandlung angeleitet, um Überlappungen zu vermeiden und Pausen in das Schulspiel zu integrieren. Für jede erledigte Aufgabe erhalten die Schülerinnen und Schüler einen Edelstein als Belohnung. Die Präsentation der Testitems und Instruktionen wurde weitgehend computergestützt umgesetzt, um eine ausreichende Durchführungsobjektivität zu erreichen.
Messinstrumente
Intelligenz
Zur Überprüfung der Intelligenz wurden jeweils 12 Testitems aus den Subtests Klassifikation (CFT-Klas), Ähnlichkeiten (CFT-Ahn) und Matrizen (CFT-Mat) des CFT-1 (Weiß & Osterland, 1997) sowie die dazugehörigen Übungsaufgaben und Instruktionen im Sinne der FleSch-Rahmenhandlung adaptiert (N = 248, Cronbachs α = .71 bis α = .83).
Arbeitsgedächtnis (AG)
Die Arbeitsgedächtnisleistung wurde in einem neu konzipierten Aufgabenset (12 Items) erfasst. Über Lautsprecher präsentierte Gegenstandsbezeichnungen müssen von den Kindern im Testheft in einer Auswahl dargestellter Bildreihen im Arbeitsgedächtnis aufrecht erhalten, identifiziert und dann die richtige Reihenfolge vor dem Hintergrund von zwei Distraktoren angekreuzt werden. Die Anzahl der zu behaltenen Items wird im Laufe des Untertests von drei auf vier gesteigert (N = 241, α = .77).
Zahlenvergleich mündlich (ZVM) und schriftlich (ZVS)
Im ersten Teil des Subtests werden in 9 Items mündliche Zahlenvergleiche im Zahlenraum von 0 bis 100 von den Kindern vorgenommen (α = .71, N = 248). Die Zahlen werden mündlich präsentiert, die Kennzeichnung der größeren Zahl erfolgt im Testheft. Um den rein sprachlichen Input zu gewährleisten, wird der Zahlenvergleich als ein „Zahlenstreit“ zwischen einer Schnecke und einem Käfer inszeniert. Das Tier, das die größere Zahl nennt, wird im Testheft angekreuzt. Zur Differenzierung werden unterscheidbare Stimmen verwendet. Im zweiten Teil treffen die Kinder in ebenfalls 9 Items die Entscheidung über die größere Zahl aus einem schriftlich präsentierten Zahlenpaar im Zahlenraum 0 bis 100 (α = .86, N = 250).
Kontextuelle Mengenbeurteilung (MENK)
Mengen werden in situativem Bezug als „viel“, „normal“ oder „wenig“ eingeschätzt. Die insgesamt 8 Items (z.B. „12 Kugeln Eis zum Nachtisch. Ist das viel, normal oder wenig?“) werden mündlich über den Lautsprecher präsentiert. Die Kinder kreuzen im Testheft ein zuvor eingeführtes Symbol für Ihre Mengeneinschätzung an (α = .68, N = 247). Die Aufgaben beziehen sich auf den Zahlenraum 1–100.
Reihenbildung (REIHB)
Die Kinder haben die Aufgabe (6 Items), eine unvollständige Reihe von aufsteigenden Punktemengen zu vervollständigen, indem sie aus einer Auswahl von Punktemengen die richtige als Ergänzung zur dargestellten unvollständigen Reihe im Testheft ankreuzen (α = .87, N = 234).
Symbol-Mengen-Zuordnung
Im Untertest zur Symbol-Mengen-Zuordnung (α = .61, N = 248) wurde die Fähigkeit der Kinder überprüft, unstrukturiert dargestellte Mengen abzuzählen und die ermittelte Menge der zugehörigen arabischen Ziffer (aus einer gegebenen Auswahl von vier Ziffern) zuzuordnen (Mengen-Symbol-Zuordnung, (SMZZ), 4 Items, (α = .62, N = 248). Im zweiten Teil des Untertests erfolgt die Aufgabenstellung in umgekehrter Folge (SMZM). Hier wird eine Zahl vorgegeben und die passende Mengendarstellung muss identifiziert werden (α = .52, N = 249). Die Aufgaben beziehen sich auf den Zahlenraum 1–10.
Visuelles Rechnen Addition (VIRA) und Subtraktion (VIRS)
Im Untertest zum visuellen Rechnen wurden Aufgaben zum visuellen Rechnen in der Addition und Subtraktion gestellt. Unter Kenntnis und Berücksichtigung der Additions- Subtraktions- und Gleichheitssymbole soll eine Gleichung (VIRA, visuelles Rechnen Addition, α = .89, N = 235; VIRS, visuelles Rechnen Subtraktion, α = .66, N = 235) um die fehlende Punktemenge des zweiten Summanden ergänzt bzw. die Punktemenge auf einer Seite des Gleichheitszeichens (Visuelles Rechnen Subtraktion) reduziert werden. Das Teil-Ganze-Verständnis sowie das Verständnis für einfache arithmetische Symbole werden in diesem Untertest überprüft (Gesamtskala VIR, α = .83, N = 241). Die Aufgaben beschränken sich auf den Zahlenraum 1–10.
Zählfertigkeit (Vorwärts zählen, Vorgänger (VG) und Nachfolger (NF) benennen)
Die Aufgaben zur Überprüfung der Zählfertigkeit (vorwärts zählen bis zur Zahl 30, den Vorgänger und Nachfolger einer Zahl benennen) sind die einzigen Aufgaben, in denen sowohl der Input als auch der Output mündlich erfolgen. Dazu werden in einer in die Rahmenhandlung eingebettete Pause zwei sogenannte „Flüsterecken“ eingerichtet, in denen die zwei Testleiter den Kindern einzeln die Aufgaben stellen und das Ergebnis auf einem Protokollbogen vermerken. Die Raumorganisation gewährleistet, dass die Leistungen einzeln von den Kindern überprüft werden (Vorgänger benennen, 6 Items (α = .85, N = 235); Nachfolger benennen, 6 Items (α = .62, N = 235); Vorgänger und Nachfolger gesamt, 12 Items (α = .83, N = 235), Zahlenraum 1–20.
Zahlen lesen (ZL)
Nach zwei Beispielaufgaben kreuzen die Kinder zu einer mündlich per Lautsprecher präsentierten Zahl aus einer Auswahl von vier Möglichkeiten die richtige schriftlich dargestellte Zahl im Testheft an. Die Zahlen bewegen sich bei einer Anzahl von 12 Items im Zahlenraum 0–100 mit ansteigendem Schwierigkeitsgrad (α = .71, N = 250).
Zur Feststellung des mathematischen Leistungsstandes wurde am Anfang der zweiten Klasse der DEMAT 1+ (Krajewski et al. 2002) eingesetzt. Das curriculumnahe Testverfahren prüft mathematische Kompetenzen von Schülerinnen und Schülern am Ende der ersten Klasse sowie zu Beginn der zweiten Klasse in den Bereichen Mengen und Zahlen, Zahlenraum, Addition, Subtraktion, Zahlenzerlegung und Zahlenergänzung, Teil-Ganzes, Kettenaufgaben, Ungleichungen und Sachaufgaben (Retest-Reliabilität r = .65). Der DEMAT 1+ eignet sich in besonderem Maße dazu, Leistungsrückstände von Schulanfängern bezogen auf die curricular festgeschriebenen Anforderungen zu erfassen (Abb. 2).
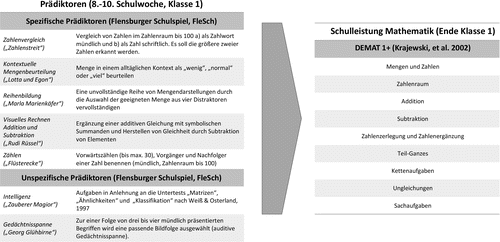
Ergebnisse
Klassifikatorische Validität des Gesamtmodells
Für die Prüfung des Gesamtmodells wurde nach dem Verfahren der logistischen Regression (Einschluss) zunächst die Klassifikationsgenauigkeit des Gesamtmodells ermittelt (vgl. Tab. 1). Als dichotomes Kriterium (y = 0/1) wurde die Mathematikleistung (rechenschwach vs. nicht rechenschwach mit PR ≤ 16 zu Beginn der zweiten Klasse definiert. Darüber hinaus wurden rechenschwache Schülerinnen und Schüler mit einem PR ≤ 10 und einem PR ≤ 25 klassifiziert.

Bezieht man im Einschluss-Verfahren alle 15 Prädiktoren in die logistische Regression ein, so ergeben sich nach Prüfung relevanter Kennwerte gute bis sehr gute Prognosemodelle (Tabelle 1). Der Omnibus-Test der Modellkoeffizienten liefert für alle drei Kriteriums-Cutoffs hoch signifikante Ergebnisse (χ2 = 80.54, df = 16, p < .001 für PR ≤ 10; χ2 = 60.56, df = 16, p < .001 für PR ≤ 16; χ2 = 70.15, df = 16, p < .001 für PR ≤ 25). Das bei der linearen Regression anschauliche Bestimmtheitsmaß R2 als Ausdruck des Anteils aufgeklärter Varianz einer abhängigen Variablen steht für die logistische Regression nicht zur Verfügung. In ähnlicher Weise kann jedoch Pseudo-R2 von Nagelkerke interpretiert werden (Backhaus et al., 2018), das sich hier für das Gesamtmodell zwischen R2 (Nagelkerke) = .45 und .54 bewegt und damit einen vergleichsweise großen Beitrag der Prädiktoren zur Trennung der Gruppen nach Kindern mit und ohne Risikostatus anzeigt. Der Hosmer-Lemeshow-Test (HL-Test) als Anpassungstest prüft, inwiefern beobachtete und vorhergesagte Fälle voneinander abweichen (Modell-Fit). Dazu wird die Stichprobe in maximal zehn Teilstichproben geteilt und die Differenzen zwischen erwarteten und beobachteten Werten auf der Basis von Chi-Quadrat intervallweise geprüft. Je geringer die Differenzen ausfallen (Bestätigung von H0, p > .05), desto besser ist die Modellanpassung. Für alle drei Prognosemodelle auf der Grundlage des gesamten Prädiktoren-Sets kann die Nullhypothese (HL-χ2 = 4.3, p = .82 für PR ≤ 10; HL-χ2 = 66.2 p < .62 für PR ≤ 16; HL-χ2 = 6.9, p < .54 für PR ≤ 25) beibehalten werden und es ist von einer hinreichenden Modellanpassung auszugehen.
Klassifikatorische Validität eines Prognosemodells nach Prädiktorenreduktion
Nach schrittweiser logistischer Regression (Kriterium-Cutoff PR ≤ 16) ergibt sich ein Prognosemodell mit vier Prädiktoren (Tab. 2). Der Omnibus-Test der Modellkoeffizienten liefert zunächst einen Gesamteindruck von der Güte des Modells. Die schrittweise Aufnahme der vier Prädiktoren (CFT-MAT, MENK, VG, ZL) führte zu einer kontinuierlichen signifikanten Verbesserung des Modells vom ersten (χ2 = 31.9, df = 1, p < 0.001) zum vierten Aufnahmeschritt (χ2 = 55.3, df = 4, p < .001). Das Pseudo-R2 von .54 (Schritt 4) fällt vergleichsweise hoch aus. Der Hosmer-Lemeshow-Test zeigt eine gute Modellanpassung (HL-χ2 = 7.22, df = 8, p = .51).
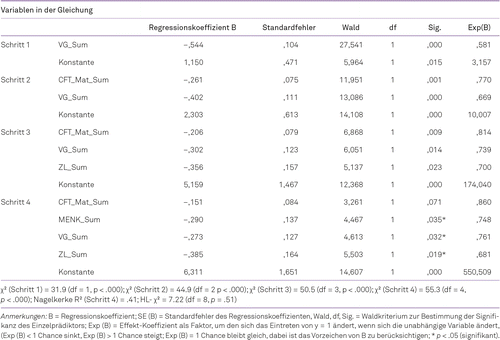
Zur Abschätzung des Einflusses der Einzelprädiktoren eignet sich für das logistische Regressionsmodell die Wald-Statistik, die zur Ermittlung der Signifikanz des B-Koeffizienten herangezogen wird. Der Effekt-Koeffizient Exp (B) gibt den Faktor an, um den sich die Chance für das Eintreten von y = 1 erhöht, wenn sich die unabhängige Variable verändert. Er kann nach 100 × (1- Exp (B)) als Wahrscheinlichkeit angegeben werden. Während die domänenspezifischen Prädiktoren MENK (100 × (1- Exp (B) = 25%), VG 100 × (1- Exp (B) = 23%) und ZL (100 × (1- Exp (B) = 32%) einen signifikanten Beitrag (p < .05) zur Trennung beitragen, verfehlt die Intelligenz (100 × (1- Exp (B) = 14%; p = .071) knapp das Signifikanzkriterium. Zur Interpretation der Bedeutung von CFT-MAT soll hier jedoch die signifikant ausfallende schrittweise Veränderung der Modellgüte im Vordergrund stehen, weil gerade bei kleineren Stichproben der Wald-Test systematisch höhere p-Werte liefert (Backhaus et al., 2018, S. 302).
Vergleicht man anhand der ROC-Analysen die Klassifizierungsleistung der Prognosemodelle auf Grundlage von 15 (Gesamtmodell, Tab. 1) gegenüber vier Prädiktoren (reduziertes Modell, Tab. 3) über alle Kriteriums-Cutoffs hinweg, so zeigen sich für Klassifizierungen nach dem Kriterium PR ≤ 16 und PR ≤ 25 mit exzellenten AUC- Werten von .84 bis .86 keine Unterschiede. Eine Ausnahme bildet die Gruppe der nach dem Kriterium PR ≤ 10 klassifizierten Kinder (AUC = .91 im Gesamtmodell gegenüber AUC = .81 im reduzierten Modell), die hier aber aufgrund der geringen Zellbesetzung in Folge der niedrigeren Grundrate nachrangig betrachtet werden sollen. Deutlich wird zweifelsfrei, dass eine Reduktion der Prädiktoren auf vier Subtests, von denen drei domänenspezifische (MENK, ZL, VG) Teilfertigkeiten und einer die allgemeine Intelligenz (CFT-MAT) betrifft, eine Trennung von Kindern nach dem Risiko-Status ebenso vornehmen kann wie die deutlich aufwändigere Prozedur von insgesamt 15 Untertests. Um dem Problem eines möglichen Stichprobeneffektes der logistischen Regressionsfunktion zu kontrollieren, wurde eine Kreuzvalidierung nach dem Holdout-Sample-Verfahren (Backhaus et al., 2018) durchgeführt, nach der im Ergebnis der ROC-Analyse (Kriteriums Cutoff PR ≤ 16) auf Grundlage der Variablengewichte der Lernstichprobe im reduzierten Modell (CFT-MAT, MENK, VG, ZL) in der Kontrollstichprobe (50%, N = 86) mit AUC = .85 (KI [.75–.95]) eine ähnlich gute Klassifizierungsgüte wie in der Lernstichprobe (N = 88, AUC = .82 (KI [.71–.93]) erreicht werden konnte.
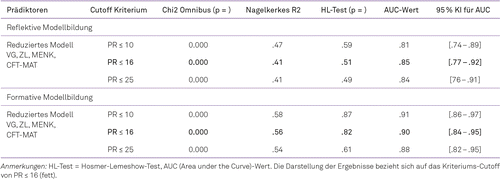
In einem nächsten Schritt sollte geprüft werden, inwiefern eine itembasierte formative Modellbildung zu einer Verbesserung der klassifikatorisch-prognostischen Validität führte.
Dazu wurden alle Einzelitems der Skalen MENK, CFT-MAT, ZL und VG in das Modell eingebracht. Um dem Problem der Parameterschätzung zu begegnen, wurden Items der Skala ZL in Anlehnung an Wollschläger (2020, S. 164f.) zusammengefasst bis keine Schätzfehler mehr auftraten. In den übrigen Skalen ergaben sich derartige Schwierigkeiten nicht.
Wie erwartet ergab sich auf der Basis eines itemgestützten formativen Messmodells gegenüber dem summativen Modell eine bessere Prognoseleistung für die alle drei Gruppen rechenschwacher Kinder unterschiedlicher Kriteriums-Cuttoffs (PR ≤ 16, PR ≤ 25, PR ≤ 10), die sich in höheren AUC-Werten zwischen .88 und .91ausdrückt. Der direkte Modellvergleich (PR ≤ 16) ergab einen signifikanten Unterschied zugunsten des formativen Ansatzes (AUC-Differenz = −0.051, KI [−0.105–0.004], z = −1.82, p (einseitig) < .05). In allen Modellen zeigte sich nach dem Hosmer-Lemeshow-Test durchgehend eine gute Modellanpassung (p > .05) (Tab. 3). Gegenüber der reflektiven Modellbildung auf Subtestebene ergab sich dadurch eine Steigerung der Klassifikationsleistung des Prognosemodells, so dass die Hypothese 3 nach diesen Ergebnissen ihre Bestätigung findet.
Güte-Kennwerte der Prognosemodelle
Grundsätzlich geht mit höherer Sensitivität immer eine abnehmende Spezifität einher (Tröster, 2009). Die Wahl des geeigneten Cutoffs bleibt daher abzuwägen. Auf der Basis des formativen Messmodells auf Itemebene (MENK, CFT-Mat, ZL, VG) konnten die Güte-Kennwerte der klassifikatorischen Vorhersage für Kinder mit schwachen Rechenleistungen (PR ≤ 16) ermittelt und in den Vergleich zu den Güte-Indizes auf der Grundlage des reflektiven Modells (Subtest-Ebene) gestellt werden (Tab. 4).
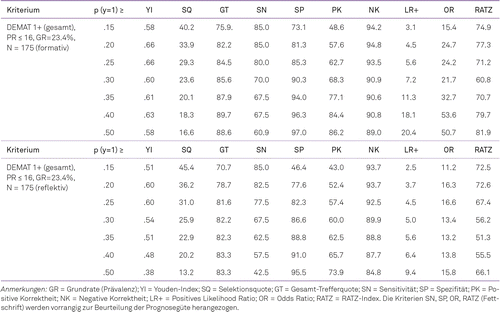
Insgesamt liefert das formative Messmodell bessere klassifikatorische Güte-Kennwerte. So können bei einem Risiko-Cutoff von p (y = 1) ≥ .20 eine Trennung (YI = .66) von Risiko- und Nicht-Risiko-Kindern mit einer Sensitivität von SN = 85% und einer Spezifität von SP = 81.3% erreicht werden. Ein Anteil von 18% falsch-positiven Screening-Befunden dürfte mit dem Anliegen eines Filterscreenings, an das sich weitere gezielte Diagnose-Maßnahmen anschließen und erst dann gezielte Fördermaßnahmen eingeleitet werden, als akzeptable Fehlerquote gelten. Die Sicherheit des Screenings liegt mit dem positiven Likelihood Ratio (LR+) von 4.5 im mäßigen Bereich (Tröster, 2009). Darüber hinaus stützen die Maße der positiven Korrektheit von PK = 62.7% und der negativen Korrektheit NK = 93.5% die Angaben zur Sicherheit. Der RATZ-Index von 77.3% im sehr guten Bereich und drückt aus, um wie viel Prozent das Modell besser als der Zufall Vorhersagen treffen kann. Mit einem OR = 24.7 ist die Wahrscheinlichkeit, nach einem positiven Screening-Befund später eine Rechenschwäche zu entwickeln bei 1 zu 25.
Auf Grundlage der reflektiven Modellierung gelingt eine weniger gute Klassifizierung, die jedoch auch noch gute Ergebnisse liefert. Relevante Werte der Sensitivität und Spezifität, der RATZ-Index und die Indizes zur Sicherheit des Screenings bleiben hinter den Kennwerten nach formativer Modellierung zurück (vgl. Tab. 4).
Diskussion
Im vorliegenden Beitrag wurden Evaluationsergebnisse eines neu konzipierten Screening-Verfahrens (FleSch) zur Vorhersage von Rechenschwierigkeiten berichtet. Im Fokus stand die Frage, ob sich auch durch eine reduzierte Anzahl domänenspezifischer und allgemein kognitiver Prädiktoren, die zu Beginn der ersten Klasse erhoben wurden, der Risikostatuts eines Kindes nach einem klassifikatorischen Ansatz zuverlässig vorhersagen lässt. Dazu wurden auf der Grundlage der referierten Befundlage und relevanter theoretischer Modelle zur Entwicklung der Zahlenrepräsentationen und des mathematischen Denkens Aufgabenformate weitgehend neu konzipiert.
Des Weiteren sollte geprüft werden, ob sich die prognostische Validität des Verfahrens dadurch steigern lässt, dass statt eines reflektiven Modells die Prognose auf der Grundlage eines itembasierten formativen Messmodells modelliert wird. Schließlich sollte geprüft werden, ob zufriedenstellende Ergebnisse hinsichtlich klassifikatorischer Güte-Kennwerte zur Vorhersage von Rechenschwierigkeiten durch das Screeningverfahren FleSch mit reduzierter Anzahl von Prädiktoren geliefert werden kann.
Prognosemodell mathematischer Leistungen
Wie gezeigt wurde ist die Befundlage zur Identifizierung relevanter Prädiktoren für die Entwicklung mathematischer Kompetenzen nicht einheitlich. Im deutschen und internationalen Raum wird die Bedeutung verschiedener Teilfertigkeiten unterschiedlich bewertet. Gleichwohl scheint es möglich zu sein (vgl. Walter 2016 b, Walter, 2020; Jordan et al., 2010), auch auf der Grundlage einer überschaubaren und damit für die Praxis handhabbaren Anzahl von Aufgaben eine Risikoabschätzung für die Entwicklung von Rechenschwierigkeiten vorzunehmen. Das konnte hier bestätigt werden: ein Prognosemodell, das auf einem reduzierten Prädiktoren-Set von drei domänenspezifischen (Mengen schätzen, Zahlen lesen, Vorgänger benennen) und einer allgemein kognitiven Variable (CFT-MAT) bestand, ergab gleich gute oder bessere Vorhersagewerte (AUC = .81 bis AUC = .91) für die Klassifikation rechenschwacher Schülerinnen und Schüler wie das Gesamtmodell mit 15 Prädiktoren: Die allgemeine Intelligenz spielte dabei eine nachrangige Rolle, die vorherrschende Relevanz früher domänenspezifischer Funktionen wurde bestätigt (Aunola et al., 2004; Gomm, 2014; Jordan et al., 2007; Krajewski, 2008). Dass eine reduzierte Prädiktoren-Anzahl zu ähnlich guten Prognoseergebnissen führt wie ein breiteres Variablen-Set wurde bereits mehrfach belegt und hier ein weiteres Mal deutlich (Jordan et al., 2010, Walter, 2016b, Walter, 2020).
Theoretische Einordnung der Befunde
Neben dieser rein empirischen Betrachtungsweise erscheint auch eine theoretische Einordnung das Modell zu legitimieren: Die drei domänenspezifischen Prädiktoren sprechen exakt die drei relevanten modularen Zahlenrepräsentationen an, die von Aster (2005) in Anlehnung an das Triple-Code Modell (Dehaene, 1992) für die wesentlichen Zahlenverarbeitungsmodule und deren wechselseitiger Transkodierungsrouten beschreibt. Mit dem Zahlenlesen werden die auditiv-sprachliche Repräsentation (das gesprochene Zahlwort) sowie das Funktionieren der Transformation eines auditiv-sprachlichen Inputs in eine visuell-arabische Notation (die arabische Ziffer) erfasst (von Aster, 2005). Das Benennen des Vorgängers einer Zahl lässt sich der Zählfertigkeit (auditiv-sprachliche Repräsentation) zuordnen und bildet hier ein auf die Entwicklung bezogene hierarchiehöhere Teilprozedur ab (Fuson, 1988), die zu dem hier angelegten Zeitpunkt der Prädiktorenerhebung bereits einige Wochen nach Schulanfang der ersten Klasse einen besonders hohen Beitrag zur Risikoabschätzung eines Kindes leistet. Mit der Aufgabe der kontextuellen Mengenbeurteilung wird der Aspekt der Zahlraumvorstellung angesprochen, der sich auf die Ausbildung einer inneren (analogen) Repräsentation von Größen bezieht. Eine Anzahl im situativen Kontext richtig einzuschätzen, erfordert eine Vorstellung von Mengen und deren relative Beurteilung.
Bedeutung unspezifischer Prädiktoren
Offen bleibt die eingangs deutlich gemachte Bedeutung der Arbeitsgedächtnisleistung, die sich sowohl in nationalen und internationalen Studienergebnissen (Alloway & Alloway, 2010) als auch in Entwicklungsmodellen (Anderson, 1992; von Aster, 2005) als bedeutsamer Einflussfaktor zeigt und die hier keinen signifikanten Beitrag zur Risikoabschätzung eines Kindes für die Entwicklung von Rechenschwierigkeiten leisten konnte. Ihre Bedeutung sollte in nachfolgenden Studien und auch innerhalb der hier referierten Datenlage besondere Beachtung finden und geklärt werden. Stellt man diesem Gedanken folgend, dem hier diskutierten Modell ein zweites Modell vergleichend gegenüber, in dem CFT-MAT durch die Gedächtnisspanne (AG) ersetzt wird, ergeben sich sowohl formativ (AUC-Differenz = −.014, KI [−.046–−.018], z = −.85, p > .05) als auch summativ (AUC-Differenz = 0.002, KI [−. 021–−.024], z = 0.14, p > .05) keine signifikanten Unterschiede. Die vielfach belegte Relevanz der Gedächtnisspanne als eine Funktion des Arbeitsgedächtnisses findet darin seine Bestätigung. Einschränkend muss jedoch kritisch angemerkt werden, dass Gedächtnisvariablen, die sich allein mündlich (Zahlwortreihe rückwärts, Benenngeschwindigkeit) realisieren lassen, im Rahmen der angestrebten Gruppentestung nicht umsetzbar waren.
Formative und reflektive Modellierung
Wie erwartet ergab sich aus einer formativen Modellierung auf Itemebene der ermittelten vier Prädiktoren auf der Grundlage höherer AUC-Werte (AUC = .88 bis .91) eine bessere Klassifikationsleistung des Verfahrens, die mit höheren Gesamttrefferquoten, Sensitivitäts – und Spezifitätswerten sowie einem höheren RATZ-Index gegenüber dem reflektiven Modell einhergingen. Der Vorteil, nicht homogene Items einer Skala als Einzelprädiktoren für die Erklärung des latenten Konstrukts Rechenschwäche in die Prognose einzubeziehen (vgl. Mazzocco & Thompson, 2005), konnte hier bestätigt werden. Es ist anzunehmen, dass eine genauere Betrachtung einzelner Teilleistungen unter Berücksichtigung des Schwierigkeitsgrades, des Entwicklungsalters, des Testzeitraumes und der Operationalisierung des Kriteriums sich differenziell auswirken. Das würde auch erklären, warum Befunde hinsichtlich der Relevanz unterschiedlicher Number Sense-Aspekte uneinheitlich ausfallen. Formativen Messmodellen sollte daher eine größere Beachtung zukommen.
Nach den dargestellten Ergebnissen wird es möglich, auf der Basis von Diagnoseprozeduren, die in einem zeitlich angemessenen Umfang in der Gruppe durchführbar sind, mit dem Flensburger Schulspiel ein Screening-Instrument zu entwickeln, dass schon zu Beginn der ersten Klasse für jedes einzelne Kind eine Risikowahrscheinlichkeit dafür bestimmen lässt, im weiteren Verlauf eine Rechenschwierigkeit zu entwickeln.
Eine weitere Validierung in einer zweiten Welle (Schuljahr 2020/21) sowie eine Evaluation des Screening-Verfahrens mit dem ersten Messzeitpunkt vor Schulbeginn (etwa 2 Monate vor Schulbeginn) werden in die Gesamtentwicklung des Verfahrens einbezogen.
Limitationen
Einschränkend muss angemerkt werden, dass die Anwendung des formativen Messmodells eine größere Stichprobe erfordert, weil die Trefferquote mit zunehmender Prädiktorenzahl überschätzt werden könnte (Backhaus et al., 2018).
Zudem sollte zur Einordnung der Ergebnisse berücksichtigt werden, dass für den Prognosezeitraum pandemiebedingt unübliche Unterrichtsbedingungen mit zeitweiligem Distanzunterricht nicht die gewöhnliche Beschulungssituation abbilden. Da keine Informationen über die Leistungsentwicklung und die Unterrichtssituation vorlagen, können Effekte unter der Annahme einer inadäquaten Fördersituation nicht ausgeschlossen werden – eine Schwierigkeit, die ein grundsätzliches Problem der Validität prognostischer Aussagen darstellt und auch im regulären Präsenzunterricht Berücksichtigung finden sollte (Schabmann, Schmidt, Klicpera, Gasteiger-Klicpera & Klingbiel, 2009) In jedem Fall bedarf es der Validierung der Ergebnisse an einer unabhängigen Stichprobe, die mit der laufenden zweiten Evaluationsphase vorbereitet wird.
Eine weitere Einschränkung betrifft die gefundene tendenziell erhöhte Grundquote, die möglicherweise auf ein leicht verstärktes Auftreten von Rechenschwierigkeiten infolge langer Zeiten des pandemiebedingten Distanzunterrichts zurückzuführen ist und damit gegebenenfalls zu einer Überselektion geführt hat.
Relevanz für die Praxis
Lehrkräfte stehen zum Einschulungszeitpunkt vor der Herausforderung, Schülerinnen und Schüler in ihren Lernvoraussetzungen und Vorläuferfertigkeiten so genau einzuschätzen, dass sich daraus eine pädagogisch sinnvolle Gruppenzusammensetzung und die Planung geeigneter Förder- und Unterstützungsmaßnahmen ergibt. Vor dem Hintergrund eines grundsätzlich präventiven Ansatzes nach dem RTI-Paradigma stellen Filterscreening dazu einen wichtigen Baustein zum Einsatz um den Einschulungszeitpunkt herum dar. Nur sind die auf dem Markt verfügbaren verlässlichen Verfahren meist als zeitlich aufwändige Einzeltests konzipiert, die sich für die Praxis als zu umfangreich erweisen. Mit dem Flensburger Schulspiel wurde der Versuch unternommen, bei gleichzeitig nachgewiesener prognostisch-klassifikatorischer Validität ein Gruppenverfahren für den Einsatz am Beginn der ersten Klasse zu entwickeln, das zudem durch eine altersangemessene Rahmenhandlung dem Entwicklungsalter der Zielgruppe gerecht wird. Durch die Anwendung des Screenings lässt sich für jeden Schüler und jede Schülerin eine individuelle Risikowahrscheinlichkeit ermitteln, an die sich bei Bedarf frühzeitig weitere Diagnose- und Fördermaßnahmen anschließen.

References
(2010). Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology, 106(1), 20–29.
(1992). Intelligence and development. A cognitive theory . Oxford: Blackwell
(2005).
Wie kommen Zahlen in den Kopf? In M. von Aster J. H. Lorenz (Hrsg). Rechenstörungen bei Kindern, 13–33. Göttingen: Vandenhoeck & Ruprecht.(2005). Rechenstörungen im Kindesalter. Monatsschrift Kinderheilkunde, 153(7), 614–622.
(2009). Neuropsychologische Testbatterie für Zahlenverarbeitung und Rechnen bei Kindern – Kindergartenversion (für Kinder von 4 bis 5 Jahren) - ZAREKI-K. Frankfurt am Main: Pearson.
(2007). Rechenstörungen bei Kindern. Vorläufer, Prävalenz und psychische Symptome. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie, 39 (2), 85–96.
(2006). Young children's number sense in China and Finland. Scandinavian Journal of Educational Research, 50 (5), 483–502.
(2004). Developmental dynamics of math performance from preschool to grade 2. Journal of Educational Psychology, 96(4), 699–713.
(2018). Multivariate Analysemethoden. Eine anwendungsorientierte Einführung (15. Aufl.). Berlin: Springer.
(2005). Making sense of number sense. Implications for children with mathematical disabilities. Journal of Learning Disabilities, 38 (4), 333–339.
(1997). Grundintelligenztest Skala 1 – CFT 1. Göttingen: Hogrefe.
(2015). Early identification of reading disabilities within an RTI framework. Journal of Learning Disabilities, 48, 281–297.
(1992). Varieties of numerical abilities. Numerical Cognition, 44, 1–42.
(2008). Prädiktion von Rechenleistung und Rechenschwäche: Der Beitrag von Zahlen-Vorwissen und allgemein-kognitiven Fähigkeiten. Berlin: Logos.
(2004). Formative und reflektive Indikatoren im Forschungsprozess: Entscheidungsregeln und die Dominanz des reflektiven Modells (Schriften zur Empirischen Forschung und Quantitativen Unternehmensplanung). München: Ludwig-Maximilians-Universität.
(2009). Operationalisierung latenter Variablen. Wirtschaftswissenschaftliches Studium, 38, 125–130.
(2013). Prävalenz von Lernschwächen und Lernstörungen: Zur Bedeutung der Diagnosekriterien. Lernen und Lernstörungen, 2, 65–76.
(2020). Formative Messmodelle und Möglichkeiten ihrer Anwendung im empirisch-pädagogischen Kontext – Datengeleitete Index-Bildung mit der MARI-Methode. RWTH Aachen: Institut für Erziehungswissenschaft.
(1986). Effects of systematic formative evaluation: A meta-analysis. Exceptional Children, 53 (3), 199–208.
(Ed.). (1988). Children's counting and concepts of number (Springer series in cognitive development). New York, NY: Springer.
(2007). An evolutionary perspective on learning disability in mathematics. Developmental Neuropsychology, 32, 471–519.
(2011). Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Developmental Psychology , 47 (6), 1539–1552.
(2009). Predicting Mathematical Achievement and Mathematical Learning Disability with a Simple Screening Tool: The Number Sets Test. Journal of Psychoeducational Assessment , 27 , 265–279.
(2017). Developmental change in the influence of domain-genereal abilities and domain-specific knowledge on mathematics achievement: An eight-year longitudinal study. Journal of Educational Psychology , 109 , 680–693.
(2005): Early identification and interventions for students with mathematics difficulties. Journal of learning disabilities , 38 (4), 293–304.
(2014). Prognostische Validität mathematischer Screenings . Dissertation, Technische Universität Dortmund.
(2012). Das Response-to-Intervention-Modell als Grundlage für einen inklusiven Paradigmenwechsel in der Sonderpädagogik. Zeitschrift für Heilpädagogik , 8 , 312–322.
(2002). Bielefelder Screening zur Früherkennung von Lese-Rechtschreibschwierigkeiten (BISC) (2., überarbeitete Auflage). Göttingen: Hogrefe.
(2010). The Importance of Number Sense to Mathematics Achievement in First and Third Grades. Learning and Individual Differences, 20 (2), 82–88.
(2007). Predicting first-grade math achievement from developmental number sense trajectories. Learning Disabilities Research & Practice, 22(1), 36– 46.
(2009). Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology, 45 (3), 850–867.
(2006). Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties. Child Development, (77), 153–175.
(2010). Kognitive Basiskompetenzen und ihr Einfluss auf die Rechtschreib- und Rechenleistung. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie, 42 (1), 15–25.
(2013). Verlauf von Umschriebenen Entwicklungsstörungen: Eine 30-Monats-Follow-up-Studie. Lernen und Lernstörungen, 2, 77–89.
(2007): Cognitive predictors of single-digit and procedural calculation skills and their covariation with reading skill. Journal of Experimental Psychology, 97 (3), 220–241.
(2008). Vorhersage von Rechenschwäche in der Grundschule (2., korrigierte Auflage). Hamburg: Kovač.
(2002). DEMAT 1+. Deutscher Mathematiktest für erste Klassen . Göttingen: Hogrefe.
(2013).
Entwicklung und Diagnostik der Zahl-Größen-Verknüpfung zwischen 3 und 8 Jahren . In M. Hasselhorn A. Heinze W. Schneider U. Trautwein (Hrsg.), Diagnostik mathematischer Kompetenzen. Jahrbuch der pädagogisch-psychologischen Diagnostik (Tests und Trends, N. F., Band 11, 41–65). Göttingen: Hogrefe.(2006). Mathematische Vorläuferfertigkeiten im Vorschulalter und ihre Vorhersagekraft für die Mathematikleistungen bis zum Ende der Grundschulzeit. Psychologie in Erziehung und Unterricht , 53 , 246–262.
(2009). Early development of quantity to number-world linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year-longitudinal-study-, Learning and Instruction , 19 , 513–526.
(2015). Rechenschwäche. Grundlagen, Diagnostik und Förderung . Göttingen: Hogrefe.
(2005). Kindergarten Predictors of Math Learning Disability. Learning Disabilities Research & Practice , 20 (3), 142–155.
(2007). The precursors of mathematics learning: Working memory, phonological ability and numerical competence. Cognitive Development , 22 (2), 165–184.
(2009).
Response to intervention . In T. B. Gutkin C. R. Reynolds (Eds.). The handbook of school psychology (4th ed. S. 434–460). Hoboken (N.J.): J. Wiley.(2009). Does systematic reading instruction impede prediction of reading in a shallow orthography? Psychology Science Quarterly , 51 , 315–338.
(2018). Rechenprobleme von Grundschulkindern: Persistenz und Schulerfolg nach fünf Jahren. Lernen und Lernstörungen , 7 , 67–80.
(2018). Successful explanations start with accurate descriptions: Questionnaire items as personality markers for more accurate predictions. European Journal of Personality , 32 , 186–201.
(2000). Developmental dyscalculia: prevalence and prognosis. European Child and Adolescent Psychiatry , 9 (2), 58–64.
(2005). Developmental dyscalculia: A prospective six-year follow up. Developmental Medicine and Child Neurology , 47 , 121–125.
(2013).
Kognitive Entwicklungspsychologie des mathematischen Denkens . In M. von Aster H. Lorenz (Hrsg.). Rechenstörungen bei Kindern – Neurowissenschaft, Psychologie, Pädagogik , 141–154. Göttingen: Vandenhock & Ruprecht.(2009). Früherkennung im Kindes- und Jugendalter. Strategien bei Entwicklungs-, Lern- und Verhaltensstörungen . Göttingen: Hogrefe.
(2003). Redefining learning disabilities as inadequate response to instruction. The promise and potential problems. Learning Disabilities Research & Practice , 18 (3), 137–146.
(2008). Adaptiver Unterricht erneut betrachtet: Über die Notwendigkeit systematischer formativer Evaluation von Lehr- und Lernprozessen und die daraus resultierende Diagnostik und Neudefinition von Lernstörungen nach dem RTI-Paradigma. Zeitschrift für Heilpädagogik , 59 (6), 202–215.
(2016a). Prognostisch-klassifikatorische Aussagen von mathematischen Screening-Verfahren am Anfang der Grundschulzeit: eine Bestandsaufnahme. Heilpädagogische Forschung , 42 (1), 25–38.
(2016b). Lassen sich mithilfe des Screening-Verfahrens ZAREKI-K am Anfang der Grundschulzeit valide prognostisch-klassifikatorische Aussagen bezüglich einer späteren Rechenschwäche machen? Heilpädagogische Forschung , 42 (3), 125–141.
(2020). Ein Screening-Verfahren zur Prognose von Rechenschwierigkeiten in der Grundschule. Zeitschrift für Heilpädagogik , 71 , 238–253.
(2019). Flensburger Schulspie l – ein gruppenbasiertes Schuleingangsscreening. Unveröffentlichtes Manuskript. Europa-Universität Flensburg.
(1997). Grundintelligenztest Skala 1 – CFT 1 (5., revidierte Auflage). Göttingen: Hogrefe.
(2020). Grundlagen der Datenanalyse mit R (5. Aufl.). Heidelberg: Springer.
(2020). Early Cognitive Precursors of Children's Mathematics Learning Disability and Persistent Low Achievement: A 5-Year Longitudinal Study. Child Development, 91 (1), 7–27.